Scala Queue

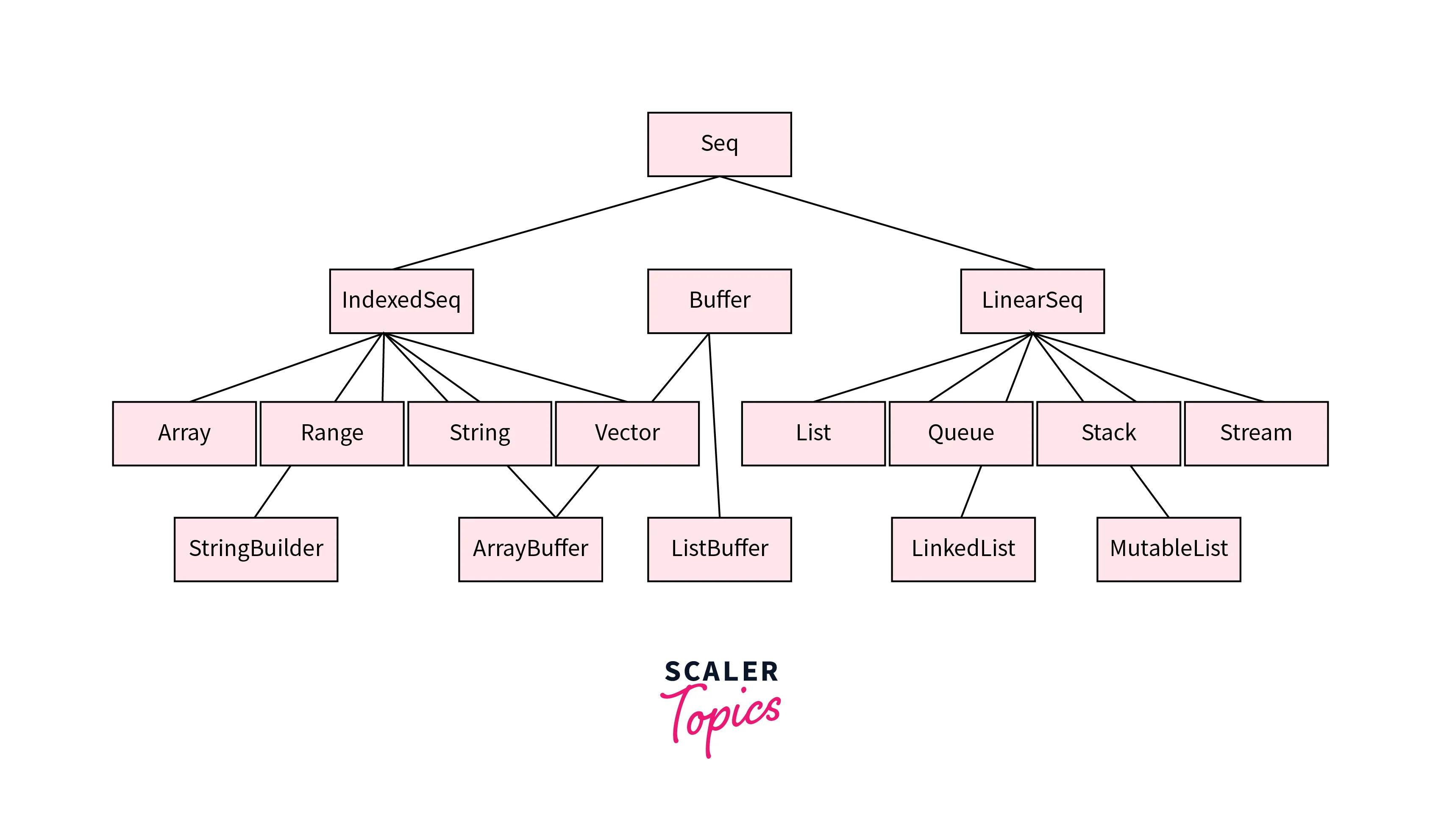
What is a Queue?

A queue is a foundational data structure that underpins various facets of computer science, operations research, and everyday scenarios. It encapsulates the notion of orderly waiting, where items are processed in the order they arrive, following the principle of First-In-First-Out (FIFO). This concept mirrors situations like people standing in a line or tasks being serviced based on their entry sequence.

Core Operations:

The core operations that define a queue are:

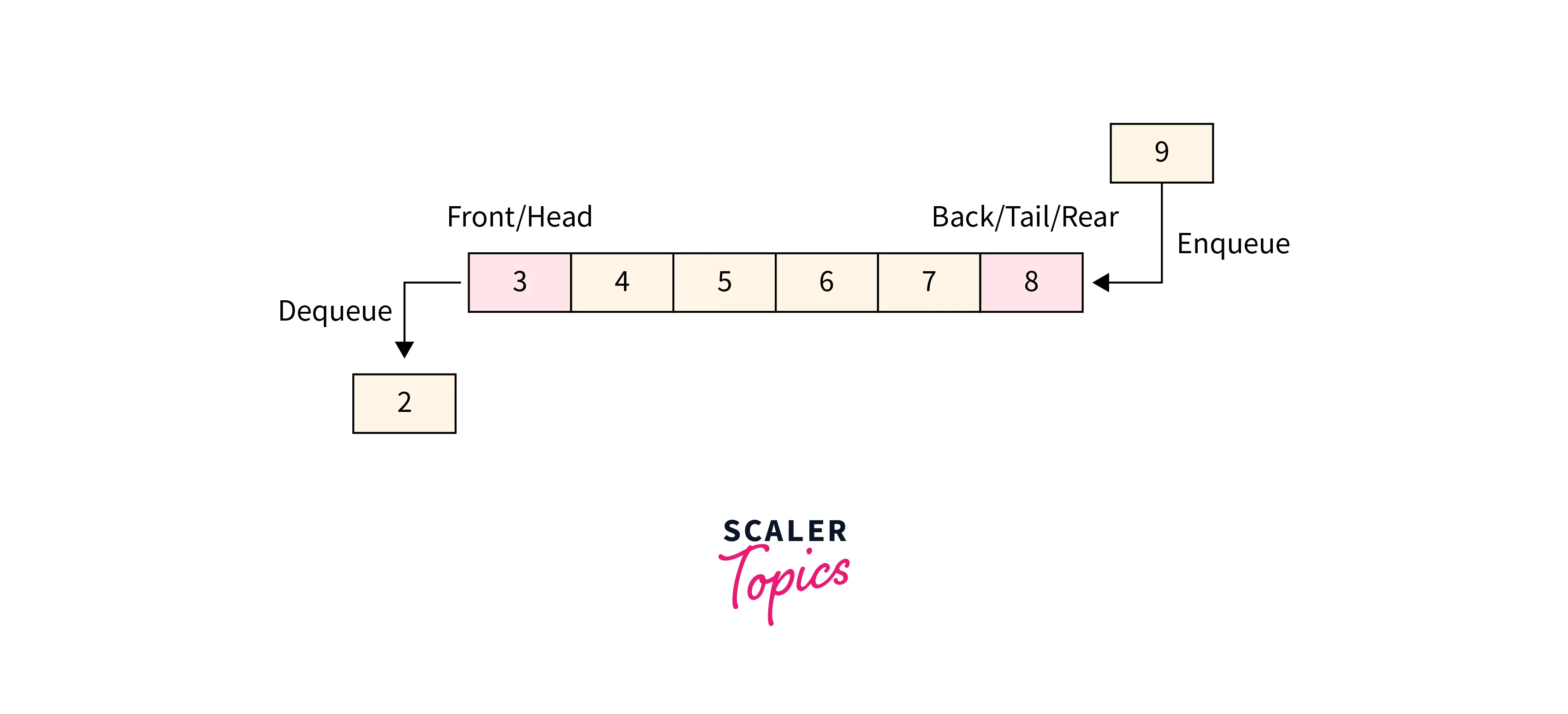
• Enqueueing:

  Enqueueing involves inserting an element at the rear end of the queue. This operation maintains the integrity of the order in which items entered the queue.

• Dequeueing:

  Dequeueing refers to the removal of an element from the front of the queue. The element that has been waiting the longest is processed and eliminated first.

Applications and Significance:

The queue data structure finds diverse applications, contributing significantly to various fields:

• Computing:

  Queues play a pivotal role in task scheduling and resource management. Operating systems employ queues to manage processes, ensuring fairness and efficient resource allocation. Printer queues handle print jobs systematically, while network queues manage data packets to prevent congestion and maintain smooth data flow.

• Algorithm Design:

  Queues are a key ingredient in graph traversal algorithms, like Breadth-First Search (BFS). BFS explores nodes level by level, ensuring thorough and systematic coverage of graph structures.

• Operations Research:

  Queuing theory, grounded in mathematical principles, provides insights into real-world systems. It aids in predicting wait times, resource utilization, and system efficiency in contexts like call centers, transportation networks, and healthcare facilities.

Implementation:

Queues can be implemented using various data structures:

• Array-based Queues:

  Utilizing arrays, items are enqueued and dequeued. Circular buffers are often employed to address wraparound challenges efficiently.

• Linked List-based Queues:

  Linked lists offer dynamic sizing and efficient memory utilization. Each element points to the next in line, ensuring order.

Types of Queues:

• Linear Queues:

  These adhere strictly to the FIFO principle, ensuring that the first element added is the first to be processed. This maintains the chronological order.

• Priority Queues:

  Priority queues deviate from strict FIFO and prioritize items based on predefined criteria, such as importance or urgency.

Benefits and Implications:

• Ordered Processing:

  Queues enforce an organized approach to processing items, making them crucial in scenarios where order matters, like task management and resource allocation.

• Algorithm Efficiency:

  Algorithms relying on queues, like BFS, enable systematic traversal of data structures, leading to efficient exploration and solution finding.

• Real-world Optimization:

  Queuing theory's insights enable the optimization of real-world systems, enhancing resource usage and minimizing wait times, thus improving user experiences.

Queues are more than a mere concept; they are a fundamental aspect of information management, algorithm design, and resource optimization

How does Queue Work in Scala?

A queue in Scala operates as a dynamic data structure that embodies the First-In-First-Out (FIFO) principle, offering an organized approach to managing elements. Understanding how a queue works involves delving into its underlying mechanics, data storage, and the principles it upholds.

Internal Structure and Enqueueing:

A Scala queue is often internally implemented using a circular buffer or dynamic array. This buffer efficiently stores elements and allows for seamless wraparound, ensuring optimal space utilization. Enqueueing, the process of adding an element to the queue, typically involves appending it to the end. If there's available space at the buffer's end, the new element takes its place there. However, when the buffer's end is full, the element might wrap around to the beginning, capitalizing on the unused space and minimizing unnecessary data shifts.

Dequeueing and Order Maintenance:

Dequeueing, the complementary operation to enqueueing, revolves around removing the front element from the queue. Just as the first person in a line is serviced first, dequeueing adheres to the FIFO principle. Behind the scenes, this operation generally involves moving the "front" pointer or index forward by one position, effectively eliminating the element from the queue. This consistent process of enqueueing at the back and dequeueing from the front ensures that the queue maintains the original order of elements.

Efficiency and Time Complexity:

Efficiency is paramount in a queue's design, particularly in scenarios where tasks need to be processed promptly. Enqueue and dequeue operations are engineered to be efficient, usually with a time complexity of O(1), meaning the time taken is constant and not dependent on the number of elements in the queue. This characteristic is crucial in applications like task scheduling and data transmission, where maintaining a streamlined order is imperative for system performance.

Advantages and Trade-offs:

Queues provide numerous advantages, particularly in scenarios where the order of processing is critical. Their adherence to the FIFO principle ensures a consistent sequence, making them useful in scenarios like print job management, process scheduling, and data streaming. However, it's important to acknowledge the trade-offs of mutable data structures like queues. In contexts where functional programming principles are essential, the mutable nature of queues may not align perfectly with the emphasis on immutability and side-effect-free operations.

Concurrency and Synchronization:

In concurrent or multi-threaded environments, queues might necessitate careful synchronization to maintain consistency. When multiple threads are enqueuing or dequeueing simultaneously, the order of operations can impact the expected behavior. Without proper synchronization mechanisms, the queue's integrity could be compromised, leading to unexpected results. Developers must be mindful of synchronization strategies to ensure reliable behavior.

Real-world Applications:

Understanding how a queue works is essential for various applications. For instance, consider a call center handling customer inquiries. Incoming calls are enqueued as they arrive, ensuring that callers are serviced in the order they contacted the center. Similarly, in transportation networks, queueing theory helps predict wait times at bus stops or airports, aiding in resource allocation and improving user experiences.

Scala queue's operation is rooted in the orderly management of elements through the principles of FIFO. Enqueueing adds elements to the back, while dequeueing removes them from the front. The internal circular buffer enhances space utilization, and efficiency is a hallmark of both operations. While queues offer advantages in maintaining order, developers must consider the trade-offs in terms of mutability and synchronization, especially in contexts that demand functional programming or concurrent environments.

Basic Operations in Queue in Scala

In Scala, the queue is represented as a collection that allows efficient addition and removal of elements while preserving their order. The two primary operations in a queue are enqueue and dequeue.

Enqueue Operation

Enqueueing involves adding an element to the back of the queue. This operation maintains the FIFO principle, ensuring that the newly added element is positioned after the existing elements, ready to be processed after the previous ones. In Scala, the enqueue operation is designed to be efficient, allowing for fast insertion of elements.

To enqueue an element in Scala, you use the enqueue method. This method takes the element as a parameter and adds it to the end of the queue. If the queue is represented using an array-based structure, the enqueue operation involves placing the new element at the end of the array. If the queue uses a linked-list-based structure, the new element becomes the last node in the linked list.

Dequeue Operation

Dequeueing is the process of removing and returning the front element from the queue. This operation maintains the FIFO order, ensuring that the first element added to the queue is the first one to be removed and processed. In Scala, the dequeue operation is designed to be efficient, with a constant time complexity, making it suitable for applications where timely processing is crucial.

To dequeue an element in Scala, you use the dequeue method. This method removes the front element from the queue and returns it. If the queue is implemented using an array-based structure, the dequeue operation involves shifting the remaining elements to fill the gap created by the removed element. If the queue uses a linked-list-based structure, the front node is removed, and the next node becomes the new front.

Working Together:

The enqueue and dequeue operations work together to provide an organized way to manage elements. Enqueueing adds elements to the back of the queue, while dequeueing removes elements from the front. This combination ensures that elements are processed in the order they were added, adhering to the FIFO principle.

Queues have various applications in computing, such as task scheduling, breadth-first search algorithms, and managing data streams. For example, in task scheduling, enqueueing tasks as they arrive and dequeueing tasks for execution ensures that tasks are executed in the order they were received.

peek()

The peek method in the Scala Queue class is used to access the element at the front of the queue without removing it. It is particularly useful when you want to examine the element that will be dequeued next, without altering the queue's state. The method signature is as follows:

Here, A is the type of elements stored in the queue. When you call peek(), it returns the element at the front of the queue, but the queue remains unchanged.

Example:

size()

The size method in the Scala Queue class returns the current number of elements present in the queue. It can be useful for checking the size of the queue before performing certain operations.

Both the peek and size methods provide valuable insights into the state of the queue without modifying its contents. These methods are helpful for implementing various algorithms and logic that involve queue operations.

Methods in Queue in Scala

Scala's Queue is a dynamic and mutable collection that adheres to the First-In-First-Out (FIFO) principle. It offers a variety of methods that allow for efficient manipulation of elements in the order they were added. These methods provide a range of functionalities, enabling tasks such as element insertion, removal, inspection, and transformation. Understanding these methods is essential for effectively working with queues in Scala.

Enqueueing Elements:

enqueue(elem: A): Unit: This method adds the specified element elem to the back of the queue, ensuring that it will be processed after the previously enqueued elements. The syntax is straightforward:

Dequeueing Elements:

dequeue(): A: The dequeue method removes and returns the front element from the queue, ensuring adherence to the FIFO order. It's essential to use this method when you need to process elements in the order they were added:

Accessing Elements: front: A: The front method provides a way to access the front element of the queue without removing it. It's particularly useful when you want to inspect the element before making a decision:

Size and Empty Check:

isEmpty: Boolean: This method returns true if the queue is empty and false otherwise. It's often used to determine if there are any more elements to process:

length: Int: The length method returns the number of elements currently in the queue. It's useful for tracking the size of the queue:

Iterating Through Elements:

`foreach[U](f: (A) => U)``: Unit: The foreach method allows you to apply a function f to each element in the queue. It's a way to perform an action on every element:

Mapping Elements:

map[B](f: (A) => B): Queue[B]: The map method applies a transformation function f to each element in the queue, creating a new queue with the transformed elements. It's useful when you need to create a new queue based on the existing one:\

Filtering Elements:

filter(pred: (A) => Boolean): Queue[A]: The filter method retains only the elements that satisfy the given predicate pred. It creates a new queue containing the filtered elements:

Appending Another Queue:

++=(xs: IterableOnce[A]): this.type: The ++= method adds all the elements from the given iterable xs to the end of the queue. It's a way to concatenate two queues:

Clearing the Queue:

clear(): Unit: The clear method removes all elements from the queue, leaving it empty: