Scan-line Polygon Filling in C

Scan-line Polygon Fill Algorithm

The Scan-line Polygon Fill method is a fundamental graphics method used to fill closed polygons on a computer screen with a certain color. This approach is critical in rendering 2D forms and pictures in various applications, including computer games, graphic design software, and CAD systems. In this section, we will go through the fundamentals of the Scan-line Polygon Fill Algorithm in C, breaking down the technical aspects into layman's terms.

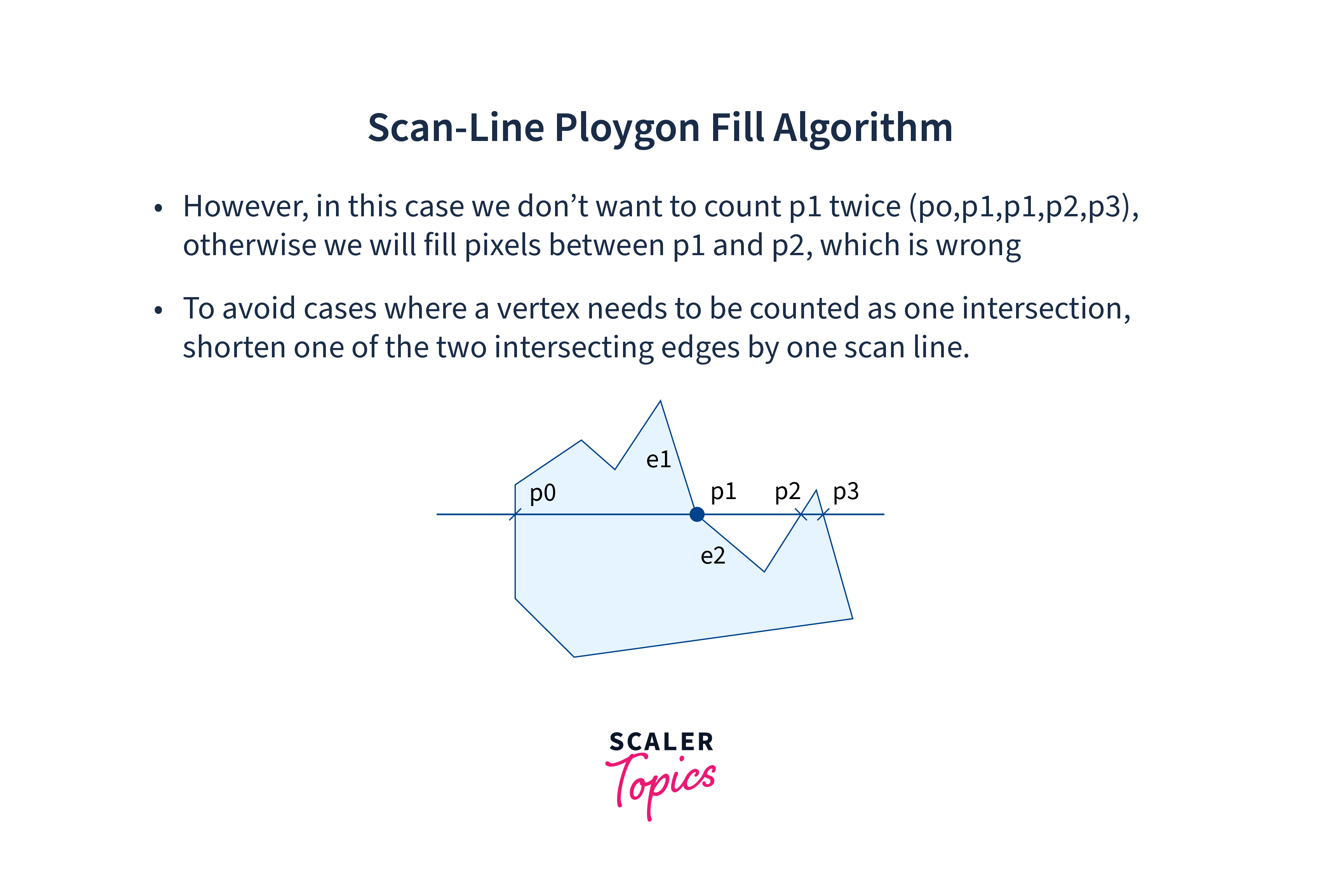
Understanding the Basics

Before diving into the algorithm itself, let's grasp the basic concepts involved:

• Polygon:

  A polygon is a closed shape with straight sides. It can be as simple as a triangle or as complex as a multi-sided figure.

• Scan-line:

  Think of a scan-line as a horizontal line moving from the top of the polygon to the bottom, pixel by pixel.

The Algorithm Steps

Now, let's outline the steps of the Scan-line Polygon Fill Algorithm:

• Initialize:

  Start by initializing a list of edges intersecting the current scan-line. This list is often called the "Active Edge Table" (AET).

• Scan-line Loop:

  Begin scanning from the top of the polygon to the bottom, moving the scan-line downward pixel by pixel.

• Edge Table Update:

  Update the AET by adding edges that intersect the current scan-line and removing edges that have crossed the scan-line completely.

• Sort Edges:

  Sort the edges in the AET based on their x-coordinates, ensuring that the edges are in the correct order for filling.

• Fill Pixels:

  Fill the pixels between pairs of edges in the AET with the desired color.

• Edge Table Update (Again):

  After filling the pixels, update the AET for the next scan-line.

• Repeat:

  Continue the process until you reach the bottom of the polygon.

Advantages of Scan-line Polygon Fill Algorithm:

• Simplicity:

  The algorithm is relatively straightforward to implement.

• Efficiency:

  It minimizes unnecessary calculations by only processing edges intersecting the current scan-line.

• Scalability:

  It can handle polygons with several sides.

The Scan-line Polygon Fill Algorithm in C is a critical tool for efficiently drawing 2D objects. By simplifying the technical complexities, this essay has helped you comprehend the fundamentals of this method. Implementing this method is critical in creating graphical apps and games that need the color-filling of complicated structures.

Components of Polygon Fill

Polygon fill, often known as scan-line fill, is an important graphics rendering technique in computer graphics. It fills closed forms with a specified color or pattern, such as polygons. Understanding the components of polygon fill is critical in C language programming for producing fast and aesthetically appealing graphics programs. In this post, we will look at the technical features of polygon fill and split them into components.

Scan-line Algorithm

The scan-line method is at the heart of polygon fill. This method examines each horizontal line of the polygon to discover whether segments of the polygon overlap with it. The contained regions are then filled with the chosen color or pattern. The scan-line algorithm is a fundamental building block of polygon fill and ensures accurate rendering.

Edge Table (ET) and Active Edge Table (AET)

Two data structures are used to handle the edges of a polygon: the Edge Table (ET) and the Active Edge Table (AET). The Edge Table contains information about the polygon's edges, including their slopes and ends. The Active Edge Table keeps track of the edges now intersecting the scan-line, allowing you to process them in the right sequence.

• Purpose of Edge Table (ET):

  The Edge Table (ET) is used to organize and store information about all the edges of the polygon that intersect the scan-line currently being processed.

• Structure:

  The ET is typically implemented as an array or linked list. Each entry in the ET corresponds to a unique edge of the polygon and contains essential information such as:

  • The edge's starting y-coordinate (Ystart).
  • The edge's ending y-coordinate (Yend).
  • The edge's x-coordinate at the current scan-line (Xcurrent).
  • The edge's inverse slope (1/m), where 'm' is the slope of the edge.
  • A pointer to the next edge in the ET.

• Purpose of Active Edge Table (AET):

  The Active Edge Table (AET) is used to keep track of the edges that intersect the current scan-line and are currently "active" or "inside" the polygon.

• Structure:

  The AET is typically implemented as a linked list. It contains entries for edges that intersect the current scan-line. Each entry stores information such as:

  • The x-coordinate of the intersection point of the edge with the scan-line (Xintersection).
  • The inverse slope (1/m) of the edge.
  • A pointer to the next edge in the AET.

The algorithm progresses by scanning the image from the bottom to the top (or vice versa), and during each scan-line, the ET is updated to include the edges intersecting the current scan-line. The AET is then used to keep track of the active edges for that particular scan-line.

As the algorithm moves from one scan-line to the next, the AET is updated to include new edges from the ET and remove edges that have finished intersecting the current scan-line. The AET helps determine the pairs of edges that define the boundaries of the filled region for that scan-line.

Sorting

Sorting the edges in the Active Edge Table is critical to ensuring that they are handled from left to right along the scan-line. This sorting phase ensures that overlapping edges are appropriately handled, avoiding visual artifacts in the filled polygon.

Sorting edges within the Active Edge Table (AET) based on their x-coordinates is crucial in scan-line polygon filling algorithms. This sorting ensures that edges are processed in the correct left-to-right order along the scan-line. Without this sorting, the algorithm may not fill the polygon accurately, resulting in missing or overfilled areas. Sorting ensures that when two edges intersect the scan-line at the same x-coordinate, the algorithm processes the leftmost edge first, preventing gaps or overlaps in the filled region. Correct edge order guarantees the algorithm's accuracy in determining the polygon's boundary and filling it correctly.

Filling Algorithm

The actual filling of the polygon is done using a filling algorithm. The "even-odd rule" or "winding number algorithm" is a popular strategy. These methods detect whether a point is within or outside of a polygon, which aids in the proper coloring of contained regions.

Color and Pattern Rendering

Once the algorithm has identified the sections to be filled, it uses the provided color or pattern to generate the polygon. This is frequently done in C language programming by altering pixel values in a frame buffer to generate the desired visual effect.

Data Structure

The Scan-line Polygon Filling Algorithm is crucial in computer graphics and picture rendering because it fills the interiors of closed forms, making them look like solid objects on the screen. This method depends on efficient data structures to manage the processing of several scan lines.

Algorithm

Before we go into the data structure, let's review how the algorithm works. The main goal is to fill in a closed polygon defined by its vertices. This is how it works:

• Initialization:

  Begin by sorting the polygon's vertices by their y-coordinates. This phase guarantees that we process scan lines from the polygon's bottom to its top.

• Edge Table:

  Create an Edge Table containing information about each polygon's edge. This table contains information such as the slope of the edge, its x-coordinate along the current scan line, and the inverse slope (1/m) to determine how the x-coordinate varies as we proceed down the scan line.

• Active Edge Table:

  Create an Active Edge Table to keep track of the edges that intersect the current scan line. This table is initially empty.

• Scan-line Processing:

  Iterate through each scan line from the polygon's bottom to its top. Add edges from the Edge Table that intersect the current scan line to the Active Edge Table during this operation.

• Filling the Scan Line:

  Sort the edges in the Active Edge Table depending on their x-coordinates once it has been updated. Then, using the current scan line, fill the pixels between pairs of edges.

• Edge Elimination:

  Remove any Active Edge Table edges with the same y-coordinate as the current scan line. To prepare for the next scan line, update the x-coordinates of the remaining edges.

• Repeat:

  Continue this procedure until all scan lines have been processed, filling the whole polygon.

Data Structures Involved

Now, let's focus on the crucial data structures used in this algorithm:

• Edge Table:

  This table is commonly implemented as an array or linked list, with each member representing a polygon edge. It maintains critical information for each edge, allowing quick access and modifications.

• Table with an Active Edge:

  The Active Edge Table, like the Edge Table, keeps a list of edges, but it changes dynamically as we move overscan lines. It is frequently implemented as a linked list or a data structure that allows for efficient element insertion and removal.

Example

Scan-line polygon filling is a basic computer graphics technique for coloring closed objects or polygons. In this post, we will dig into the complexities of scan-line polygon filling and present a practical example in C. We'll use basic terminology to guarantee that even novices understand the topic.

Before we go into the coding, let's go through the basics of scan-line polygon filling. The main concept is to divide the screen into horizontal lines (scan-lines) and find the intersections of these lines with the polygon's edges. We can efficiently fill the whole polygon by keeping track of these crossings and coloring the pixels between them.

Code

Explanation

In this code example, we've shown how to create a scan-line polygon filling in C. This approach is a fundamental building element of computer graphics and may be expanded to handle increasingly complicated graphics applications. You may start your adventure into the exciting field of computer graphics programming by comprehending the concept and studying the code.