Selection Sort in Java

Selection sort Algorithm

Selection sort is yet another sorting algorithm that is used to sort a List/Array of integers, characters, floating-point numbers, and other user-defined data structures.

Before beginning with the selection sort in java, let us first understand what is meant by sorting. Sorting means arranging elements of the array in ascending or descending order, as shown in the image below -

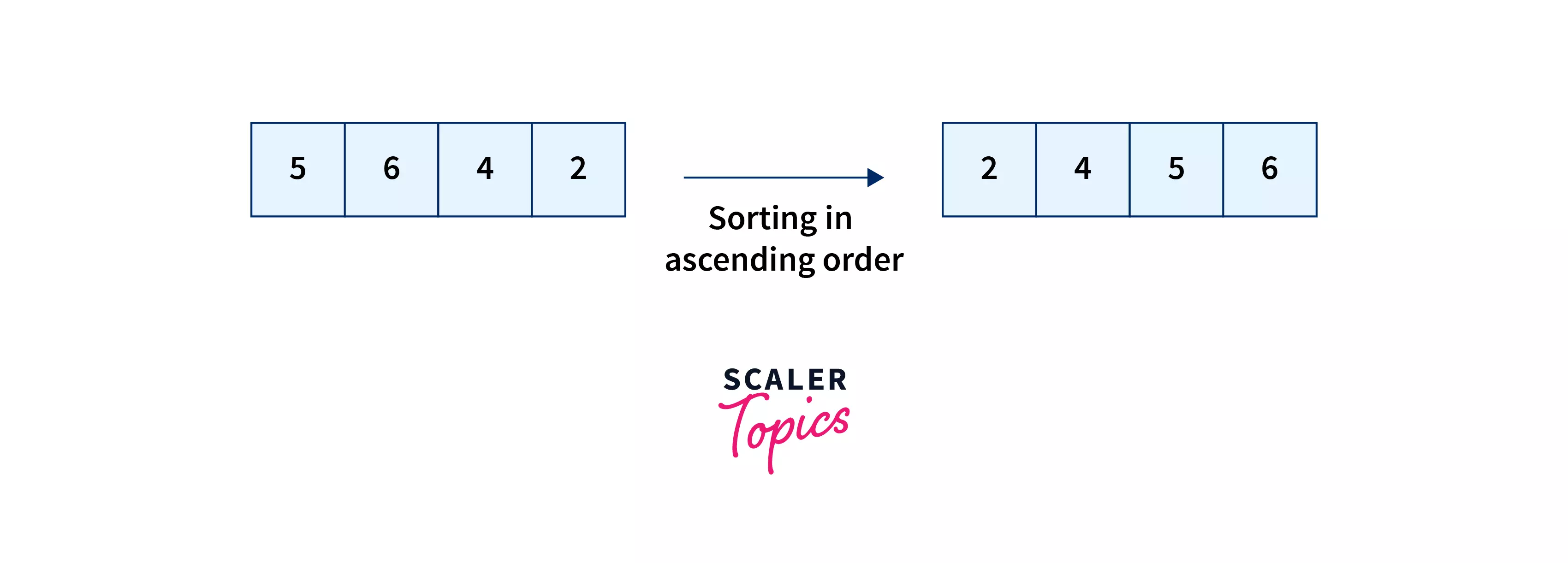
Selection sort, also known as the in-place sorting algorithm (since it does not require any extra space for sorting) is a sorting algorithm that works on the idea of repeatedly finding the smallest/largest element and placing it at its correct sorted position by swapping it with the element that is currently placed there.

Selection sort in Java works by dividing the array/list into two sublists:

• Sorted Sublist
• Unsorted Sublist

Initially, the whole array is treated as the unsorted sublist, and then with each iteration, we do the following:

• Search for the smallest element in the unsorted part.
• Put the obtained smallest element at the end of the sorted part.

Note that the above steps are to sort the array/list in ascending order; to sort in descending order, the largest element can be found in the unsorted part instead of the smallest element.

Steps involved to sort an array (say a) of size n using the selection sort algorithm are -

• For $i^{th}$ element in the array i.e. a[i]. Note that initially (i = 0), we will be considering the whole array to be unsorted.
• Find the index of the minimum element present in the unsorted array/sublist, let's say the index to be ind.
• Swap this element with the element that was at the beginning of the unsorted sublist i.e. $swap(a[i], a[ind])$.
• Repeat the above three steps for each $0<i<n$.

Example of Selection Sort

Let's say we want to sort the following array -

Now as per the algorithm discussed in the previous section, we will consider the whole array to be unsorted.

• Iteration 1 (i = 0)
  • Find the smallest element in the unsorted list i.e. $min(a[i])$ where $0\leq i<5$.
  • It can be said that the smallest element is 1 at index 3.
  • Swap $a[0] \text{ and } a[3]$.
  • Now array will look like a = [ 1, 3, 2, 9, 5 ]
• Iteration 2 (i = 1)
  • Find the smallest element in the unsorted list i.e. $min(a[i])$ where $1\leq i<5$.
  • It can be said that, smallest element is 2 at index 2.
  • Swap $a[1] \text{ and } a[2]$.
  • Now array will look like a = [ 1, 2, 3, 9, 5 ]
• Iteration 3 (i = 2)
  • Find the smallest element in the unsorted list i.e. $min(a[i])$ where $2\leq i<5$.
  • It can be said that, the smallest element is 3 at index 3.
  • Swap $a[3] \text{ and } a[3]$. (Swapping with itself will not make any change).
  • Now array will look like a = [ 1, 2, 3, 9, 5 ]
• Iteration 4 (i = 3)
  • Find the smallest element in the unsorted list i.e. $min(a[i])$ where $3\leq i<5$.
  • It can be said that, smallest element is 5 at index 4.
  • Swap $a[3] \text{ and } a[4]$.
  • Now array will look like a = [ 1, 2, 3, 5, 9 ]

The iterations end here, and it can be easily noticed that the array is sorted in ascending order now.

Selection sort program in Java

To implement the selection sort in java we will do the following steps -

• Declare the array (say a) of size n and define the values of elements present in it.
• Use a for loop to iterate from i = 0 to n-1 and in each iteration do the following
  • Initialize a variable minIndex = i
  • Iterate from j = i+1 to n and update minIndex = j if a[minIndex] > a[j]
  • Swap the values at the indices i and minIndex respectively.
• Print the sorted array.

Note that we will iterate till i < n-1 because, each time, we will look for the smallest element present in unsorted sublist $i.e.$ right side and when $i = n-1$ there will be no unsorted list; therefore, we iterate till i < n-1.

Output

This selection sort algorithm will also work for the array that is not pre-defined $i.e.$ user has to input the values present in the array. In the below-given code, user needs to enter n, which will denote the size of the array, and then he/she needs to enter n number of elements.

Output

Complexity Analysis

• Time Complexity : As we can see that, there are two nested for loops, each of which can run for $O(n)$ time. Also, it can be noticed that in every case (iteration of the outer loop), the inner loop will run for $n$ times (or for the remaining number of elements), and hence the time complexity `of selection sort in java in the best case, worst case, and the average case is $O(n^2)$.

• Space Complexity : We are not using any extra space to sort the array hence we can say the space complexity of selection sort in java is $O(1)$.

The time complexity is same for every case (best, worst and average) because each time, we need to find the minimum element so that it can be placed in the correct position, and we have to trace the complete array for that.

For more details on the Selection sort algorithm, please visit the article on the Selection Sort.

Learn More

• Time Complexity of Selection Sort