C++ Program for Sieve of Eratosthenes

Transform Your Career

Choose from our industry-leading programs designed for career success

NSDC Certified

Modern Software and AI Engineering Program

Master full-stack development with AI integration

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

NSDC Certified

Modern Data Science and ML with specialisation in AI

Advanced data science techniques with AI specialization

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

NSDC Certified

Advanced AIML with Specialisation in Agentic AI

Deep dive into AIML with focus on Agentic systems

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

NSDC Certified

DevOps, Cloud & AI Platform Engineering

Build and manage AI-powered cloud infrastructure

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

NSDC Certified

AI Engineering Advanced Certification by IIT-Roorkee

Premier AI engineering certification from IIT-Roorkee

3 MonthsDuration

AI-LedCurriculum

Career SupportSupport

Go to Program

What is the Sieve of Eratosthenes?

Before moving on to the Sieve of Eratosthenes algorithm, let's first talk about prime numbers.

Prime numbers are positive integers divisible only by 1 and itself. In other words, prime numbers can't be divided by other numbers than itself or 1. For Example, 2, 3, 5, 7, 11, 13, 17, etc. The above numbers can only be divided evenly by 1 or itself, so they are the prime numbers.

Sieve of Eratosthenes is an efficient algorithm for finding all the prime numbers in a given range.

The algorithm works iteratively by marking the multiples of each prime as non-primes (composite) because we are sure that if any number is a multiple of some other number, then it can never be prime. For Example, if 2 is a prime number, then all the multiples of 2 (i.e., 4, 6, 8, 10, 12, 14, 16.. and so on) are composite numbers as they are multiple of 2, so they can never be prime. We will repeat this process until we are left with no next prime number in the list. Once all the multiples of each discovered prime have been marked as composites, the primes are the remaining unmarked numbers in the list.

Learn more about sieve of eratosthenes

Concept of Sieve Of Eratosthenes:

Instead of checking every number as prime(brute force approach), we would work on the groups, and the main concept behind this algorithm is that a number is said to be prime if none of the smaller prime numbers divides it. Since we are iterating over a list of numbers, we already marked all the numbers as non-primes, which are multiple of any other number. Hence, if we reach a cell that is not marked, it isn't divisible by any smaller prime number and therefore has to be the prime number. At last, we can scan a range of numbers given in the input. Let's say the given range is [l..r], then we can iterate from l to r and check the numbers which are not marked as false (as they will be the prime numbers), and then, we can include them in our resultant set as primes.

Algorithm

To find all the prime numbers less than or equal to a given integer n by sieve of the Eratosthenes method, the following steps are to be followed as listed below:

• Create a boolean array of size n, and mark all the elements as true`, assuming all the numbers are primes in the starting.
• Then, start the loop from 2 as it is the smallest and the first prime number. Let's denote it by p and mark all the numbers divisible by it as false (as they will be composite numbers).
• We will find all the numbers divisible by it by enumerating its multiples of p by counting in increments of p from 2p to n and marking them false in the list. The integer p * m should not be marked.
• Now, find the smallest number in the list greater than p that is not marked (which means it is the next prime number).
• If there was no such number, stop.
• Otherwise, let p now equal this new next prime number, and repeat the same step of enumerating and marking its multiples as false.
• We will continue this until we are left with no next prime number in the list (which means all the remaining are marked as false).
• When the algorithm terminates, all the numbers remaining in the list that are not marked as false are all prime numbers below n.
• We will add all the prime numbers in the resultant set and print them.

Let's understand the above algorithm with the help of an example:

Suppose we want to print all prime numbers smaller than or equal to 50.

We create a list of all numbers from 2 to 50, marked in green (which means they are marked as true initially(all are primes)):

Now, according to the sieve of the Eratosthenes algorithm, we will mark all the numbers divisible by 2 and by counting in increments of 2 as false (denoted by red in the diagram).

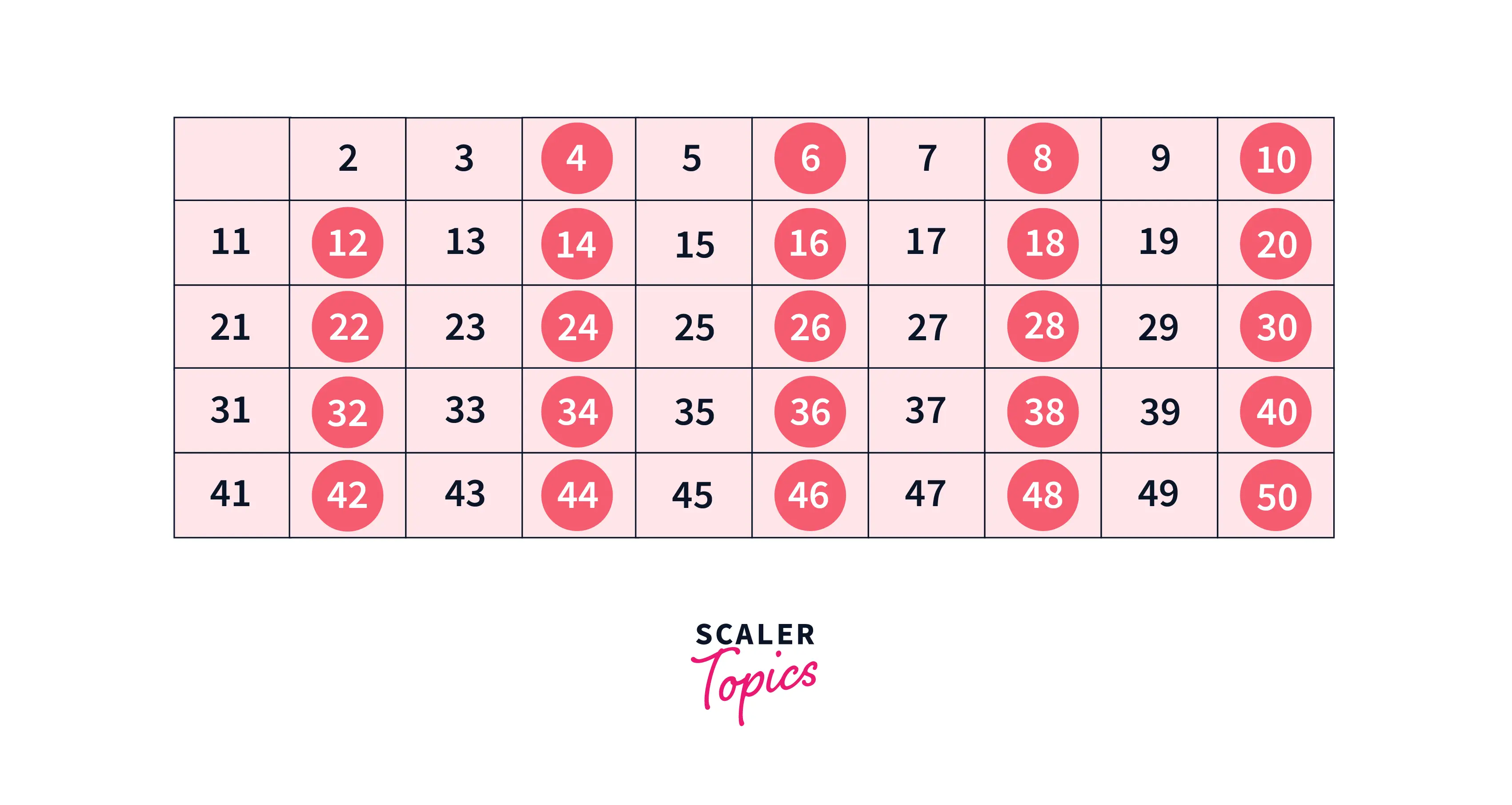
Now, we will move to our next unmarked number, the prime number 3, and mark all the numbers which are multiples of 3 in a similar way we did for 2.

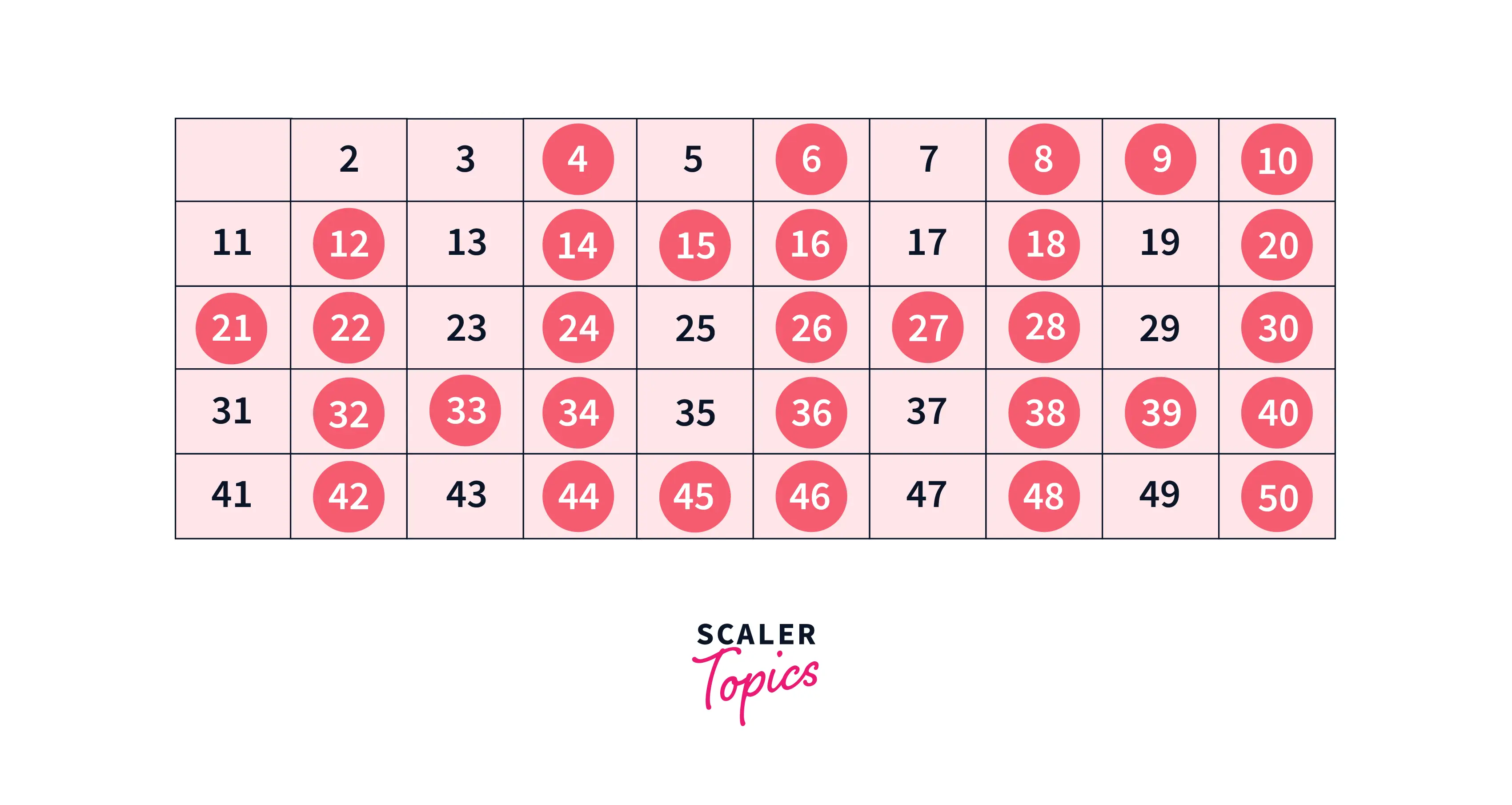
We will now move to our next unmarked number, 5, and mark all multiples of 5 as false.

We will continue this process until we are left with no next prime number in the list. Our final table will look like this:

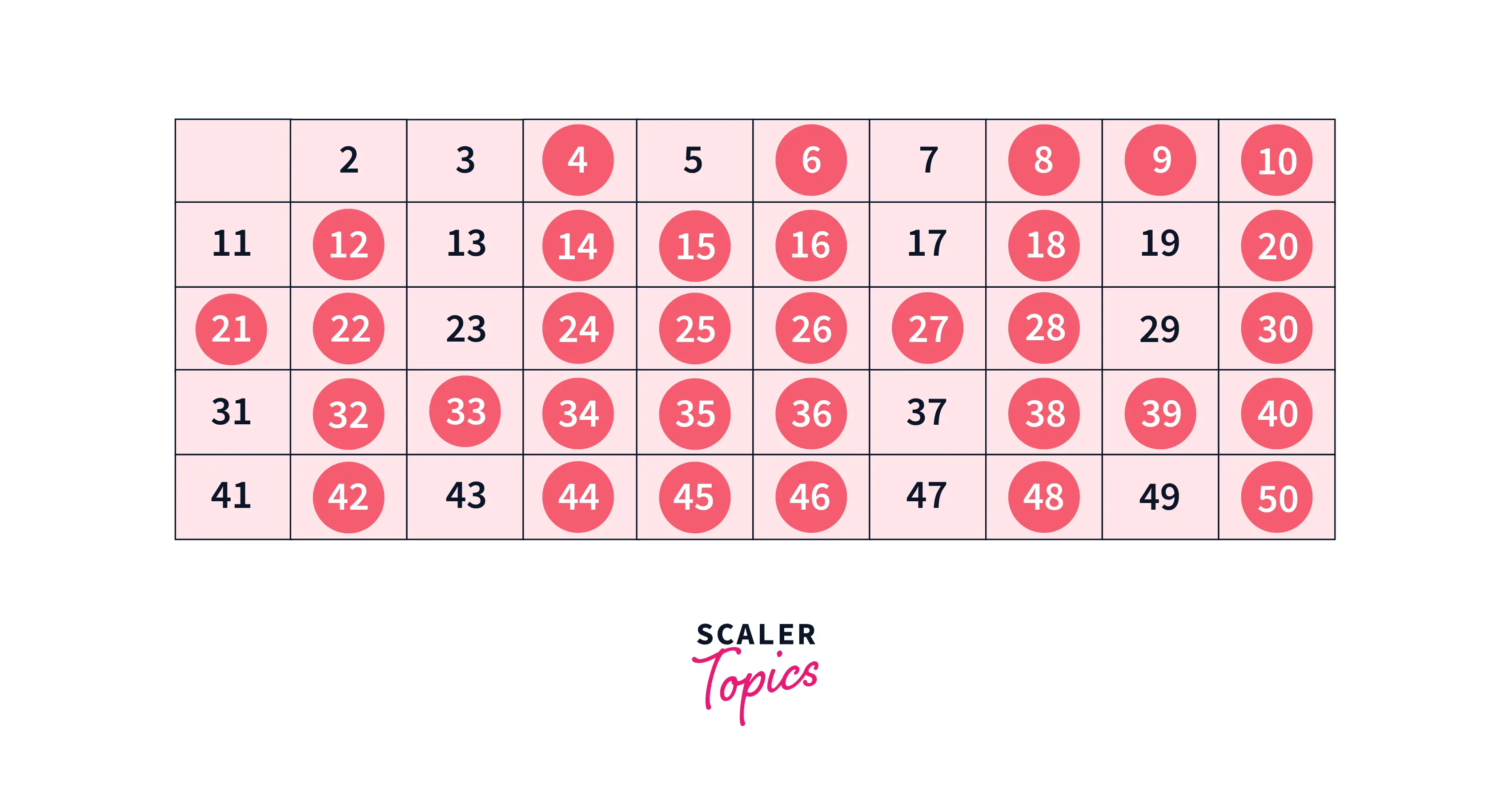
So, the unmarked numbers (or those marked as true) are the prime numbers. In this table, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, and 47 are the primes.

Hiring Partners:

GoogleAmazonMicrosoftFlipkartAdobe1200+ more

C++ Program to Implement Sieve of Eratosthenes:

Example: Let's take a simple example for understanding how to implement the sieve of the Eratosthenes algorithm:

Suppose we want to print all prime numbers smaller than or equal to 30.

We create a list of all numbers from 2 to 30, marked in green (which means they are marked as true initially(all are primes)):

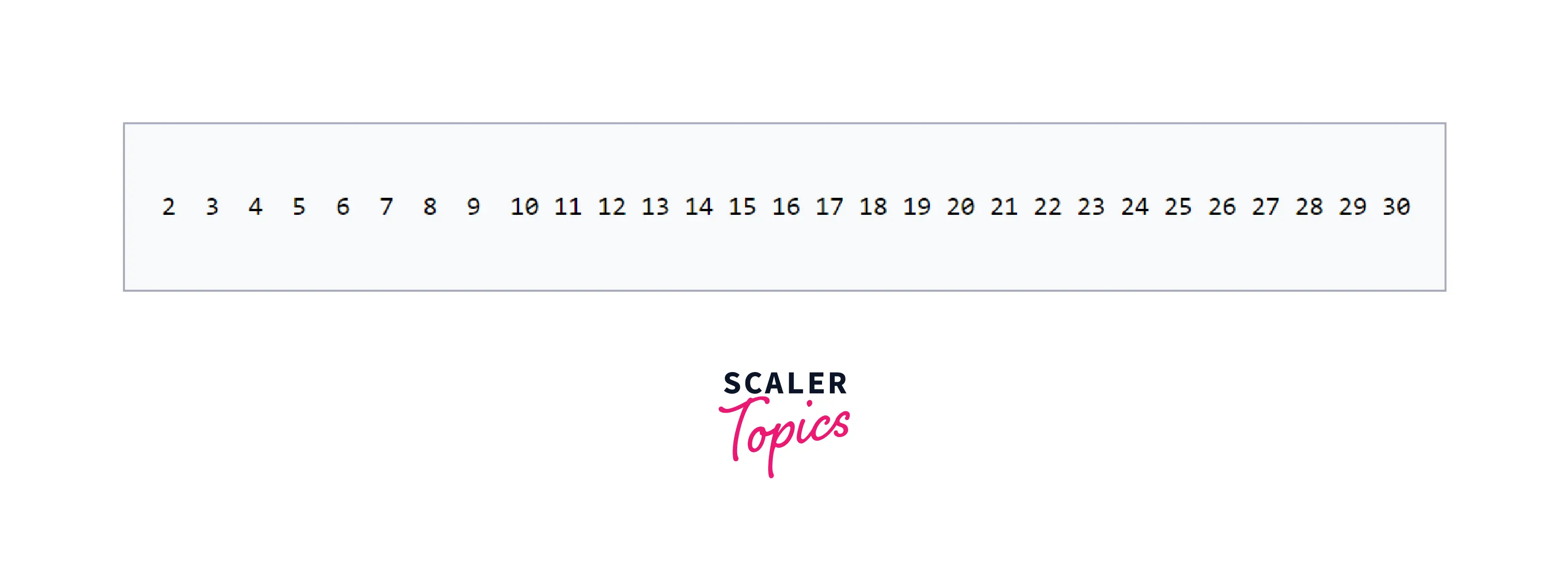
Now, according to the sieve of the Eratosthenes algorithm, we will mark all the numbers divisible by 2 and by counting in increments of 2 as false (denoted by red in the diagram).

Now, we will move to our next unmarked number, the prime number 3, and mark all the numbers multiples of 3, similar to what we did for 2.

We will now move to our next unmarked number, 5, and mark all multiples of 5 as false.

We will continue this process until we are left with no next prime number in the list, and the unmarked numbers (or those marked as true) are the prime numbers. In this table, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 are the primes.

Let's write a program to implement the sieve of the Eratosthenes algorithm:

Output:

Explanation: As you can see from the above program, we have been given an integer n, we need to implement a sieve of the Eratosthenes algorithm to find all the prime numbers up to n. Initially, we created a boolean array of the size n and initialized all the entries as true, meaning all the numbers are considered prime. Then, we started with the smallest prime number, i.e., 2, and marked all the multiples of 2 as false as we were sure they couldn't be prime (because they are divisible by some other number). We will repeat this process by moving to the next prime number in the list until we are left with no such next prime number in the list.

In the end, we will traverse the range from 2 (as 2 is the smallest prime number ) tonand print all the numbers marked as true to be the prime numbers.

Complexity:

Time and Space Complexity Analysis:

Time complexity: The inner loop runs n/2 + n/3 + n/5 + … n/97…, so it performs n / i steps, where i is prime, so the whole complex is $sum(n / i) = n * sum(1/i)$.

According to the prime harmonic series, the sum (1/i) where i is prime is $log(log n)$.

So the overall time complexity is $O(n * log(log(n)))$.

Space complexity: Boolean prime array has been used in the code, contributing to the auxiliary space. Hence, the space complexity of the above code is $O(n)$.

Program for Sieve of Eratosthenes to Generate Prime Numbers Between Given Range:

Let's write a program to generate prime numbers between a given range. Suppose we have a lower limit L and an upper limit R, and we have to print all the prime numbers within this given range (between L and R).

Algorithm:

The algorithm is the same as we discussed above; we will:

• Assume that all the numbers in the range are prime, and we will mark them as true in the starting.
• In the following steps, we will look at the first marked number, considering this to be a prime number.
• Then, we will change all the multiples of this prime number in the range between l and r given in the input (l and r are integers, l <= r) to false, as we are sure these numbers are composite and can't be primes.
• We will repeat this process until we are left with no such next prime number in the list (which means all the remaining numbers are marked as false).
• In the end, all the numbers marked as true are the prime numbers in the given range.

Example Let's take a simple example of finding prime numbers between L and R, where L = 10 and R = 30:

Output:

Explanation: As you can see from the above program, we have been given two integers L and R, and we have to print all the prime numbers between L and R. Initially, we have created a boolean array of the size (R + 1) and initialized all the entries as true, which means that all the numbers are initially considered as primes. Then, we started with the smallest integer prime number, i.e., 2, and changed all the multiples of 2 to false, as we know that if a number is a multiple of any other number, then it can't be prime. Now, we will move to the next prime and mark all its multiples as false, as they are composite numbers, not prime. We will repeat this process until we are not left with any number marked as true in the upcoming iterations.

In the end, we will traverse the range from L to R and print all the numbers marked as true as the prime numbers.

Complexity:

Time and Space Complexity Analysis:

Time complexity: The inner loop runs $r/2 + r/3 + r/5 + … r/97…$, so it performs r / i steps, where i is prime, so the whole comp is $sum(r / i) = r * sum(1/i)$.

According to the prime harmonic series, the sum (1/i) where i is prime is $log (log (r - l + 1))$.

So the overall time complexity is $O((r - l + 1) * log(log(r - l + 1)))$, where r is the upper limit in the given range.

Where l is the lower limit and r is the upper limit of the range given in the input.

Space complexity: Boolean prime array has been used in the code, contributing to the auxiliary space. Hence, the space complexity of the above code is $O(r - l + 1)$.