Smoothing in Image Processing

Introduction

Smoothing in image processing refers to the process of reducing noise or other unwanted artifacts in an image while preserving important features and structures. The goal of smoothing is to create a visually appealing image that is easy to interpret and analyze. Smoothing techniques use various algorithms, such as filters or convolutions, to remove noise or other distortions in the image. Effective smoothing requires striking a balance between removing unwanted artifacts and preserving important image details, and is an essential step in many image processing applications, including image segmentation, object recognition, and computer vision.

Types of Smoothing Filters

Smoothing filters, also known as blurring filters, are a type of image filter that are commonly used in image processing to reduce noise and remove small details from an image. There are several types of smoothing filters, including mean filter, median filter, Gaussian filter, and bilateral filter.

Mean Filter

The mean filter is a type of linear smoothing filter that replaces each pixel in the image with the average of its neighboring pixels. The size of the neighboring pixels is defined by the filter kernel or mask. The larger the kernel, the stronger the smoothing effect. Mean filters are easy to implement and are commonly used in low-level image processing tasks such as noise reduction and edge detection. However, they tend to blur edges and details in the image, leading to loss of image quality.

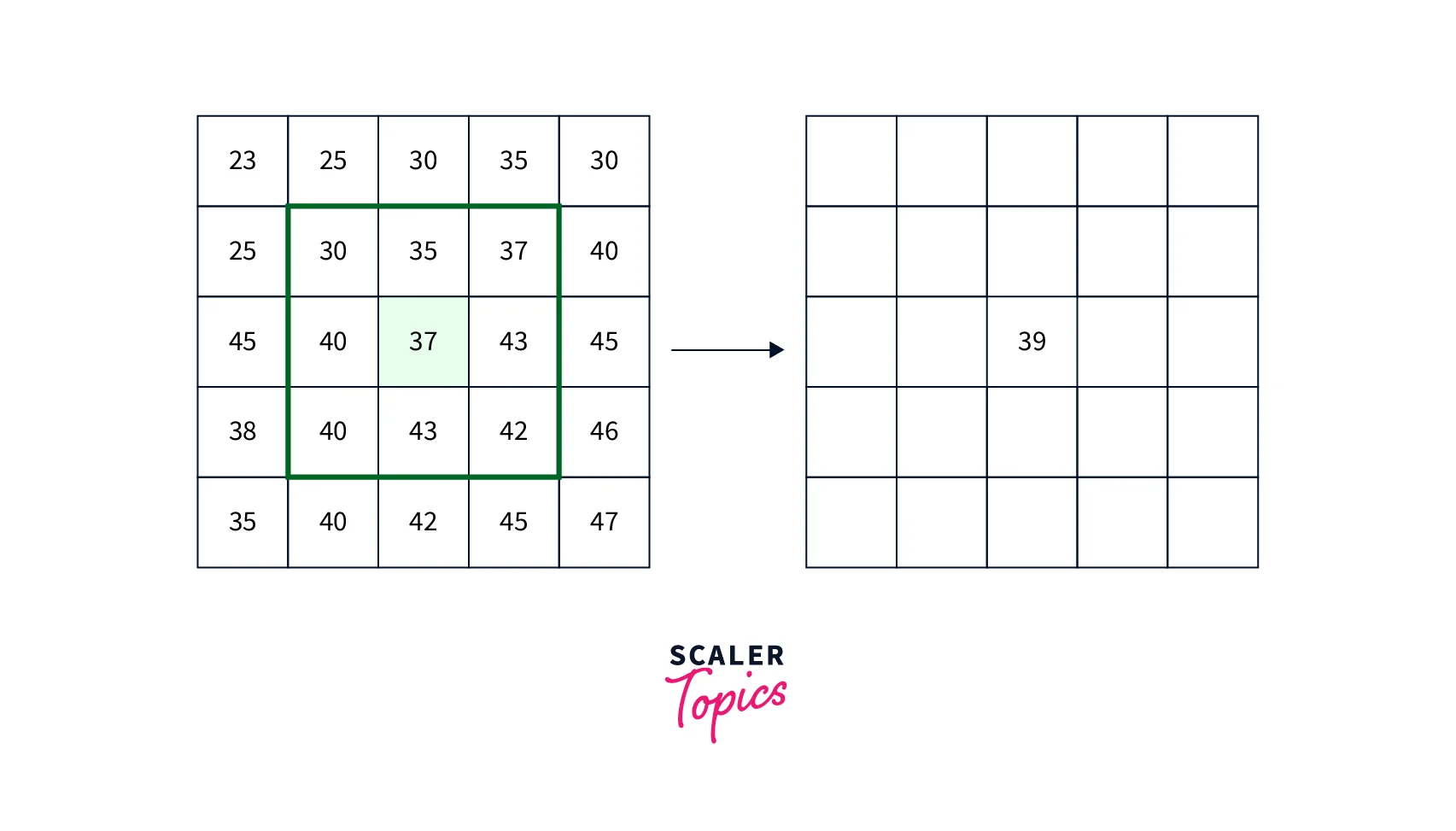
Median Filter

The median filter is a type of nonlinear smoothing filter that replaces each pixel in the image with the median value of its neighboring pixels. The size of the neighborhood is also defined by the filter kernel. Unlike the mean filter, the median filter does not blur edges and details in the image. Instead, it preserves them while removing the noise. Median filters are commonly used in image processing tasks that involve removing salt and pepper noise from the image.

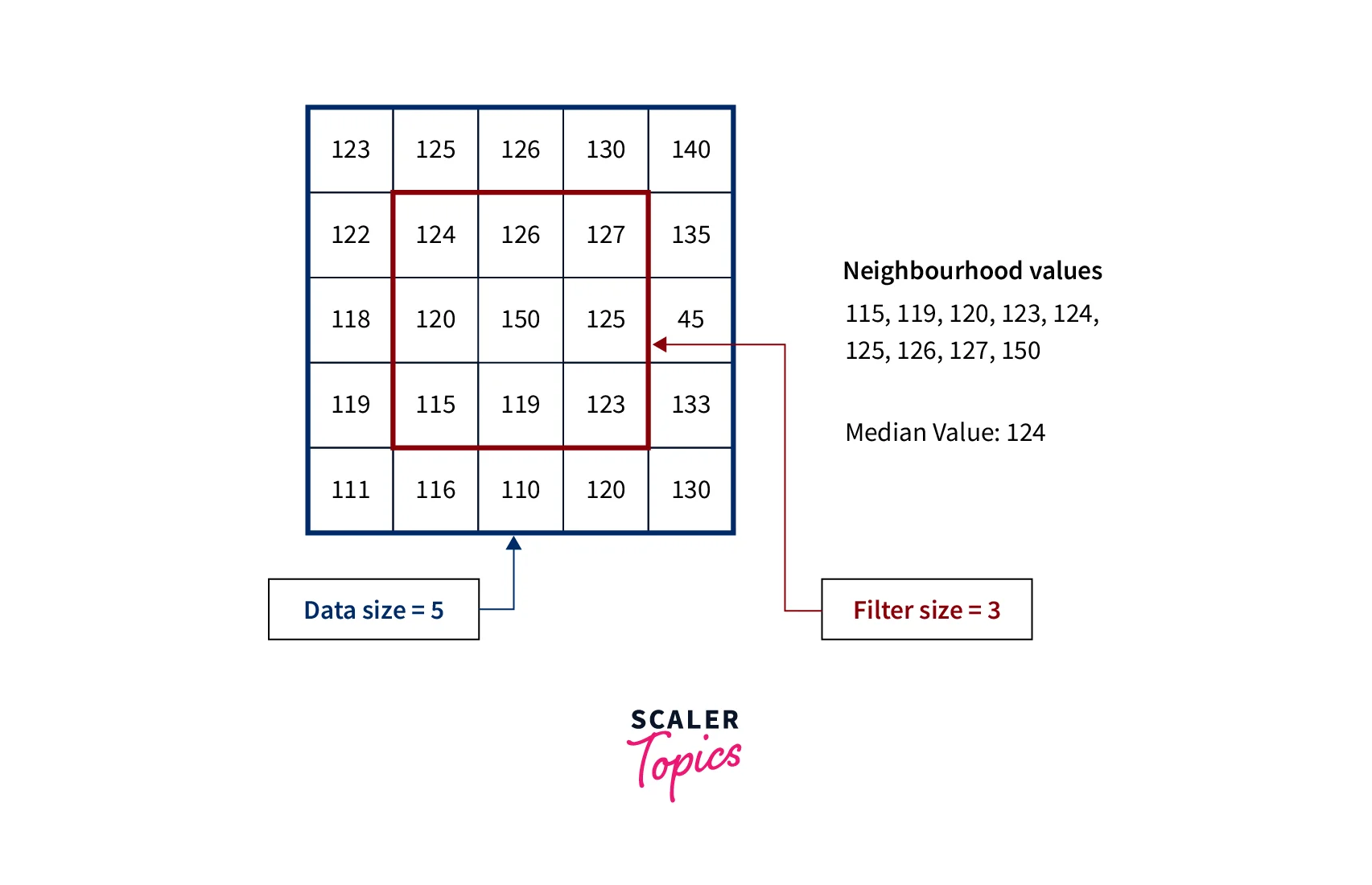
Gaussian Filter

The Gaussian filter is a type of linear smoothing filter that is based on the Gaussian distribution. The filter works by convolving the image with a Gaussian kernel. The Gaussian kernel has a bell-shaped curve that determines the weight of each pixel in the neighborhood. Pixels closer to the center of the kernel have a higher weight than pixels farther away. The Gaussian filter is a good choice for smoothing images while preserving edges and details. However, it is computationally expensive and can produce ringing artifacts around edges.

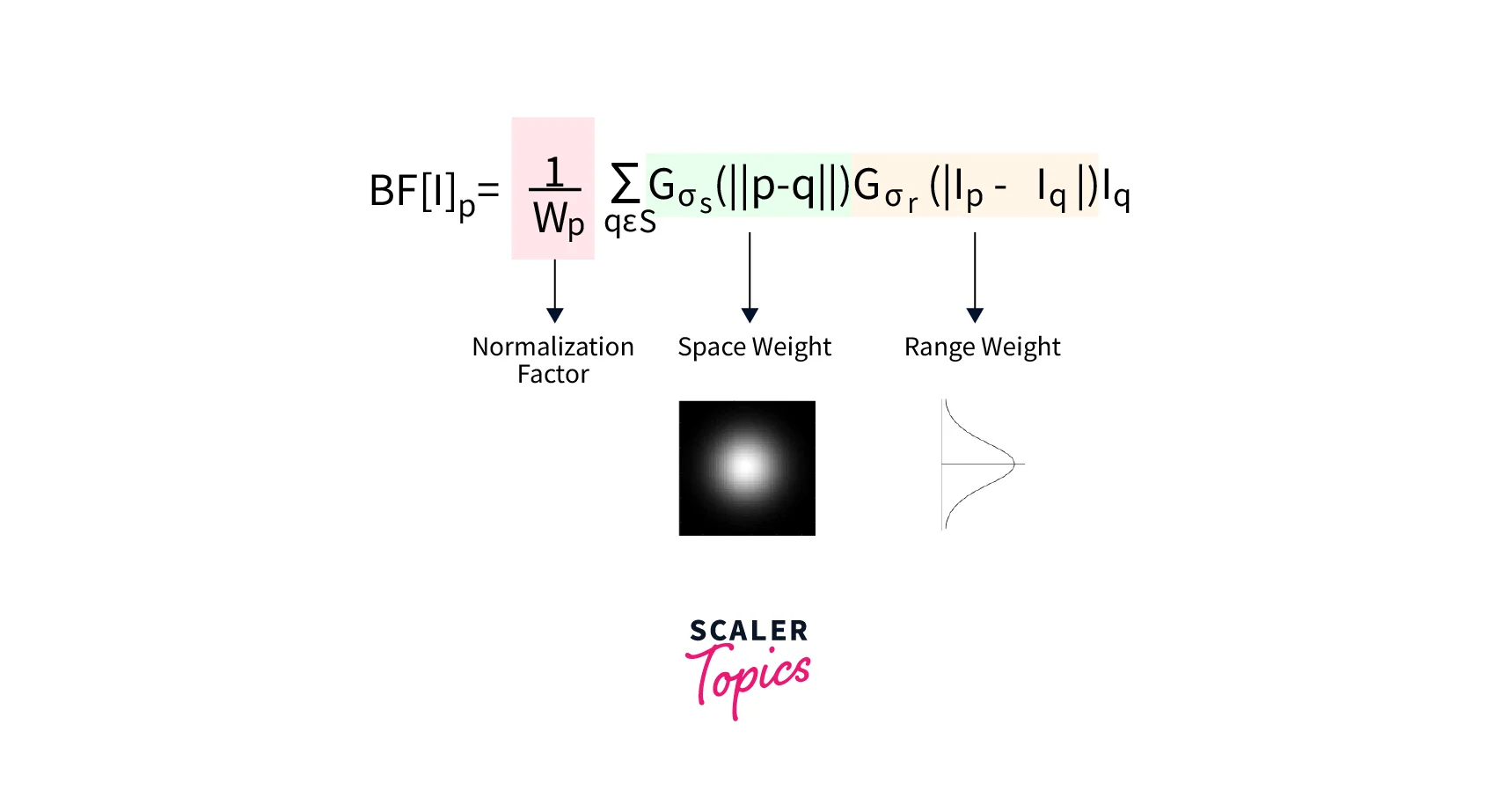
Bilateral Filter

The bilateral filter is a type of nonlinear smoothing filter that uses a combination of spatial and range filtering. The spatial filter is similar to the Gaussian filter, while the range filter is based on the difference in pixel intensities. The bilateral filter preserves edges and details while removing noise. It is commonly used in image processing tasks such as image denoising, edge-preserving smoothing, and tone mapping.

Smoothing Techniques

Convolution-Based Techniques (eg., Applying Filters to An Image)

Convolution-based techniques involve applying filters to an image to smooth out noise and sharp edges. This is achieved by convolving the image with a filter kernel, which is a small matrix of values. The filter kernel is moved across the image, and at each location, the pixel values are multiplied by the corresponding values in the kernel, and the sum of the products is used to replace the original pixel value.

Common filter kernels for smoothing include the Gaussian filter, which assigns a weight to each pixel based on its distance from the center of the kernel, and the mean filter, which replaces each pixel with the average of the surrounding pixels. Other types of filters can be used to achieve different effects, such as edge detection or sharpening.

Non-Local Means Techniques (eg., Using Similar Patches from Other Parts of The Image)

Non-local means techniques involve using similar patches from other parts of the image to smooth out noise. This is based on the idea that pixels that are close together in value and location are likely to be part of the same object or texture, and therefore smoothing should be applied based on the similarities between patches rather than individual pixels.

The non-local means algorithm works by calculating a weighted average of the pixels in a patch, where the weights are based on the similarity between the patch being smoothed and other patches in the image. The algorithm compares the patches using a distance metric, such as the Euclidean distance or the L1 norm, and assigns a weight to each patch based on its similarity to the patch being smoothed.

Wavelet-Based Techniques (eg., Applying Wavelet Transforms to An Image)

Wavelet-based techniques involve applying wavelet transforms to an image to decompose it into different frequency bands. The high-frequency bands represent the details of the image, such as sharp edges and noise, while the low-frequency bands represent the overall structure and smooth variations.

Smoothing can be achieved by filtering out the high-frequency bands and reconstructing the image using only the low-frequency bands. This can be done using a thresholding approach, where coefficients in the high-frequency bands that are below a certain threshold are set to zero, or a soft-thresholding approach, where coefficients that are below the threshold are reduced in magnitude by a certain amount.

Wavelet-based techniques are often used for image compression and denoising, as they can preserve important features while reducing the size of the image or removing unwanted noise.

Applications of Smoothing

Smoothing, also known as image filtering or image smoothing, is a technique used to remove noise and other unwanted artifacts from images. This technique can be applied to various types of noise, including salt-and-pepper noise and Gaussian noise. Smoothing is also used for edge preservation, pre-processing, and aesthetic purposes.

Noise Reduction (eg., Removing Salt-And-Pepper Noise, Gaussian Noise)

Smoothing is commonly used to reduce noise in images. Noise can be caused by various factors, including poor lighting, poor camera settings, and other environmental factors. Salt-and-pepper noise is a type of noise that appears as isolated pixels in an image, either completely white or completely black. Gaussian noise, on the other hand, is a type of noise that appears as a random pattern of light and dark pixels. To remove these types of noise, a smoothing filter can be applied to the image. This filter averages the pixel values in the image, reducing the impact of isolated pixels and random patterns. There are various types of smoothing filters, including mean filter, median filter, and Gaussian filter, each with its own strengths and weaknesses.

Edge Preservation (eg., Smoothing an Image While Preserving Edges)

When smoothing an image, it's important to preserve the edges in the image. Edges are the boundaries between different regions in the image, such as the boundary between the sky and the mountains in a landscape photograph. If edges are lost during the smoothing process, the image can appear blurry or unclear. To preserve edges during the smoothing process, a filter can be applied that selectively smooths areas of the image that are away from edges, while leaving the edges untouched. Examples of edge-preserving filters include bilateral filter, guided filter, and anisotropic diffusion filter.

Pre-Processing (eg, Preparing an Image for Further Processing)

Smoothing can also be used as a pre-processing step before applying other image-processing techniques, such as segmentation or feature extraction. For example, if an image is very noisy or has a lot of texture, it can be difficult to accurately identify objects in the image. By smoothing the image first, the noise and texture can be reduced, making it easier to identify objects in the image.

Aesthetic Purposes (eg, Creating a Blurred Background Effect)

Smoothing can be used for aesthetic purposes, such as creating a blurred background effect in a portrait photograph. By selectively smoothing the background of the image, the subject of the photograph can be made to stand out more. Similarly, smoothing can be used to create a painterly effect in an image, giving it a more artistic look and feel.

Algorithms for Smoothing

Standard Algorithms (e.g., Box Filter, Median Filter)

Standard algorithms for smoothing are a set of techniques that can be used to reduce noise in signals or images. These algorithms are often simple and efficient, and they can be implemented quickly on a computer. Two common types of standard algorithms for smoothing are the box filter and the median filter.

Box filter

• The box filter, also known as the average filter, is a technique used to smooth signals or images by averaging the values in a neighborhood around each pixel. The neighborhood is usually defined by a rectangular or square window, and the size of the window determines the degree of smoothing. The box filter is a linear filter, meaning that the output is a weighted sum of the input values.

Median filter

• The median filter is a non-linear filter used to remove noise from signals or images. Instead of averaging the values in a neighborhood around each pixel, the median filter replaces each pixel with the median value in its neighborhood. The median filter is often more effective than the box filter at removing noise while preserving edges and other features in the image.

Machine Learning-Based Algorithms (e.G., Deep Neural Networks)

Machine learning-based algorithms for smoothing are a set of techniques that use artificial neural networks to learn how to remove noise from signals or images. These algorithms are often more complex than standard algorithms, but they can be more effective at removing noise and preserving features in the image.

Deep neural networks

• Deep neural networks are a type of machine learning algorithm that can be used for smoothing. These networks are designed to learn the relationship between inputs and outputs through multiple layers of processing. In the case of smoothing, the inputs are noisy signals or images, and the outputs are the smoothed signals or images. The network is trained on a dataset of noisy and clean signals or images, and it learns to map the noisy inputs to the clean outputs.
• Deep neural networks can be designed in many different ways, and there are many variations that can be used for smoothing. For example, some networks use convolutional layers to process images, while others use recurrent layers to process time-series data. Some networks also incorporate additional constraints, such as sparsity or smoothness, to improve the quality of the output.

Implementation of Smoothing in Image Processing

Smoothing, also known as blurring, is a common image processing technique used to reduce noise or to remove small details from an image. There are several types of smoothing techniques, including

How to perform Media Blur with OpenCV?

Median blur is a non-linear smoothing technique that replaces each pixel in an image with the median value of its neighboring pixels. This technique is effective in reducing salt-and-pepper noise in an image while preserving the edges. To perform median blur in OpenCV, we can use the cv2.medianBlur() function, which takes the input image and the size of the kernel as input parameters.

How to perform Bilateral Blur with OpenCV?

Bilateral blur is a non-linear smoothing technique that preserves the edges while smoothing the image. This technique is effective in reducing Gaussian noise in an image while preserving the edges. To perform bilateral blur in OpenCV, we can use the cv2.bilateralFilter() function, which takes the input image, the size of the kernel, the sigma value for color space, and the sigma value for the spatial space as input parameters.

Gaussian Blur

Gaussian blur is a linear smoothing technique that convolves the image with a Gaussian kernel. This technique is effective in reducing Gaussian noise in an image while smoothing the image. To perform Gaussian blur in OpenCV, we can use the cv2.GaussianBlur() function, which takes the input image, the size of the kernel, and the sigma value for the X and Y direction as input parameters.

Box Blur

Box blur is a linear smoothing technique that convolves the image with a box kernel. This technique is effective in reducing uniform noise in an image while smoothing the image. To perform box blur in OpenCV, we can use the cv2.boxFilter() function, which takes the input image, the depth of the output image, the size of the kernel, and the flag for normalization as input parameters.

Challenges and Future Direction

Smoothing, also known as blurring, is a fundamental operation in image processing that is widely used for noise reduction, edge detection, and feature extraction. However, there are several challenges associated with smoothing in image processing, including:

1. Trade-off between smoothing and detail preservation:
   One of the main challenges in smoothing is to find the right balance between reducing noise and preserving the important details in the image. Over-smoothing can lead to the loss of important details and edges, while under-smoothing can leave noise and artifacts in the image.
2. Computational complexity:
   Some smoothing techniques, such as bilateral filtering and non-local means filtering, are computationally expensive and can take a long time to process large images or video streams. This can be a challenge in real-time applications that require fast and efficient processing.
3. Parameter tuning:
   Many smoothing techniques have several parameters that need to be tuned for optimal performance, such as the kernel size, filter type, and sigma values. Tuning these parameters can be time-consuming and requires expertise in image processing.

In terms of future directions, there are several research areas that are currently being explored in smoothing in image processing, including:

1. Deep learning-based smoothing:
   Deep learning techniques, such as convolutional neural networks (CNNs) and generative adversarial networks (GANs), have shown promising results in smoothing images and removing noise. These techniques can learn the optimal smoothing parameters from large datasets and can be used to perform complex smoothing tasks.
2. Real-time smoothing:
   Real-time smoothing is becoming increasingly important in applications such as video processing and computer vision. Researchers are developing new algorithms and hardware architectures to enable fast and efficient smoothing in real time.
3. Multi-scale smoothing:
   Multi-scale smoothing involves applying different smoothing techniques at different scales to preserve both the large-scale and small-scale features in an image. This approach has shown promising results in preserving important details while reducing noise and artifacts.