B Tree Index

Let's look at an example to see which queries can benefit from a B-Tree Index. Assume you have the following table:

The following is a basic outline of its structure:

The index for the above table will include the values from the first name, the last name, and the dob columns for each row in the table. The index will sort the data based on the order of the columns specified above. If two people have the same name but different birth dates, they will be ordered by birth date.

Now that we know how B-tree works let's look at the types of queries that will benefit from B-tree indexes.

• Match the entire amount: A full key value match defines values for all columns in the index. For example, this index can assist you in locating a person called Vikas Gupta, who was born on November 13, 1979.
• Match a leftmost prefix: This index will assist you in locating all people with the surname. This just makes use of the index's first column.
• Match a column prefix: This function can help you identify all people whose last names begin with A. This just makes use of the index's first column.
• Match a set of values: Can locate anyone with the surnames Gupta or Garg.

B-Tree Drawbacks

B-Tree indexes have several drawbacks. A B-Tree will not assist if:

• The lookup does not begin on the left side of the indexed columns. For example, the above index will not assist you in identifying persons named Vikas or people born on a specific day because such columns are not in the index's leftmost position. Similarly, the above index cannot be used to locate people whose surnames begin with something.
• Any column specified in the index is skipped. That is, you cannot use a person's last name and date of birth to find them since, in this situation, the first name is missed.
• Any condition can be utilized after a range condition.  Since LIKE is a range condition, the index access will only use the first two columns in the index in a query where the condition is lastname = 'gupta' and firstname like 'V%' and dob = '13-11-1979′.

How Is Indexing Used in a Database?

When it comes to database indexing, the B-tree data structure becomes a little more sophisticated by having not just a key, but also a value linked with the key. This value points to the actual data record. A payload is the combination of a key and a value.

Assume the three-column table below must be stored in a database.

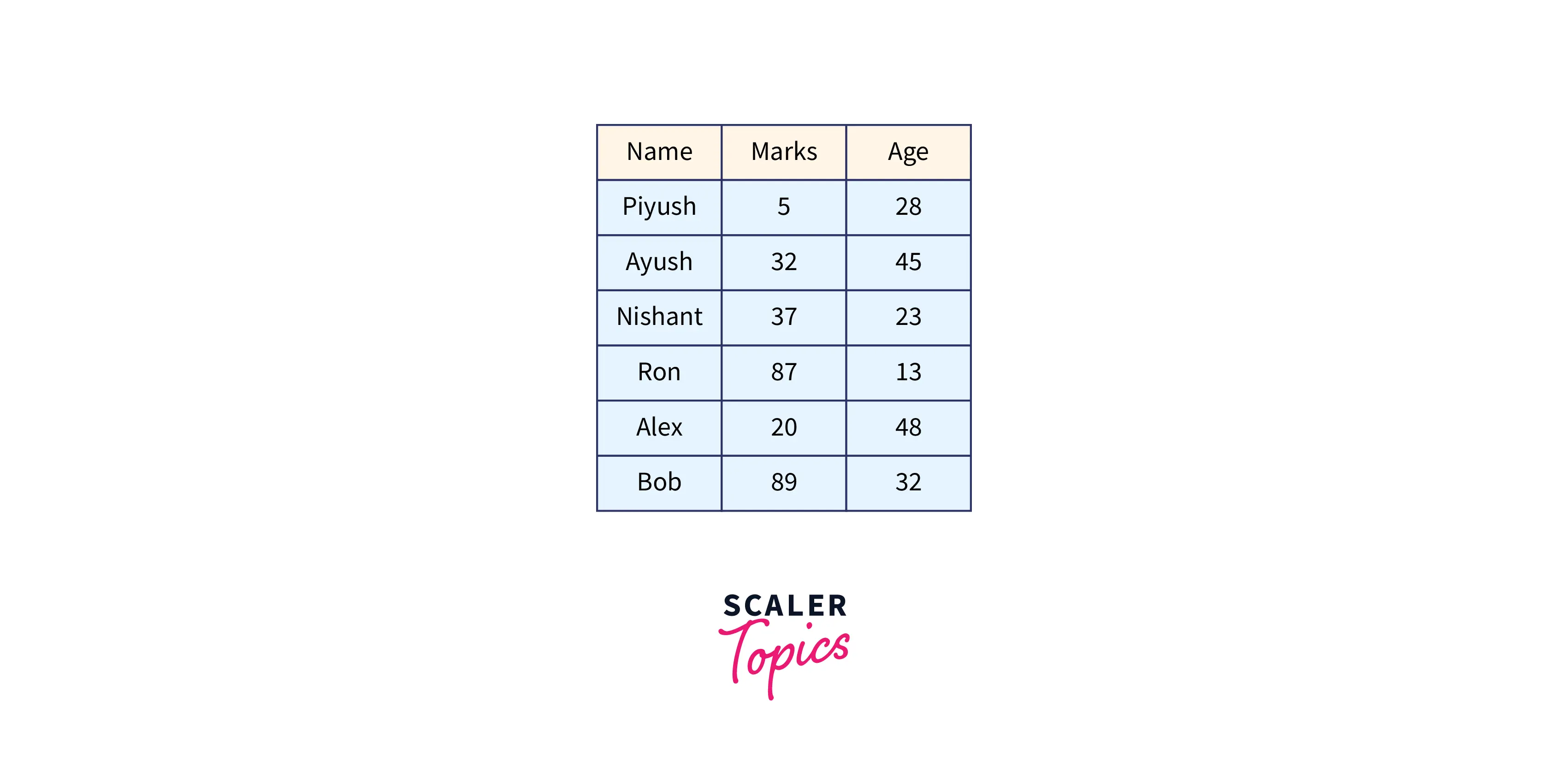
The database first generates a unique random index (or primary key) for each of the given records and turns the relevant rows into a byte stream. The keys and record byte streams are then stored on a B+tree. The random index is used as the indexing key in this case. Payload refers to the key and record byte streams as a whole. The resulting B+tree can be illustrated as follows.

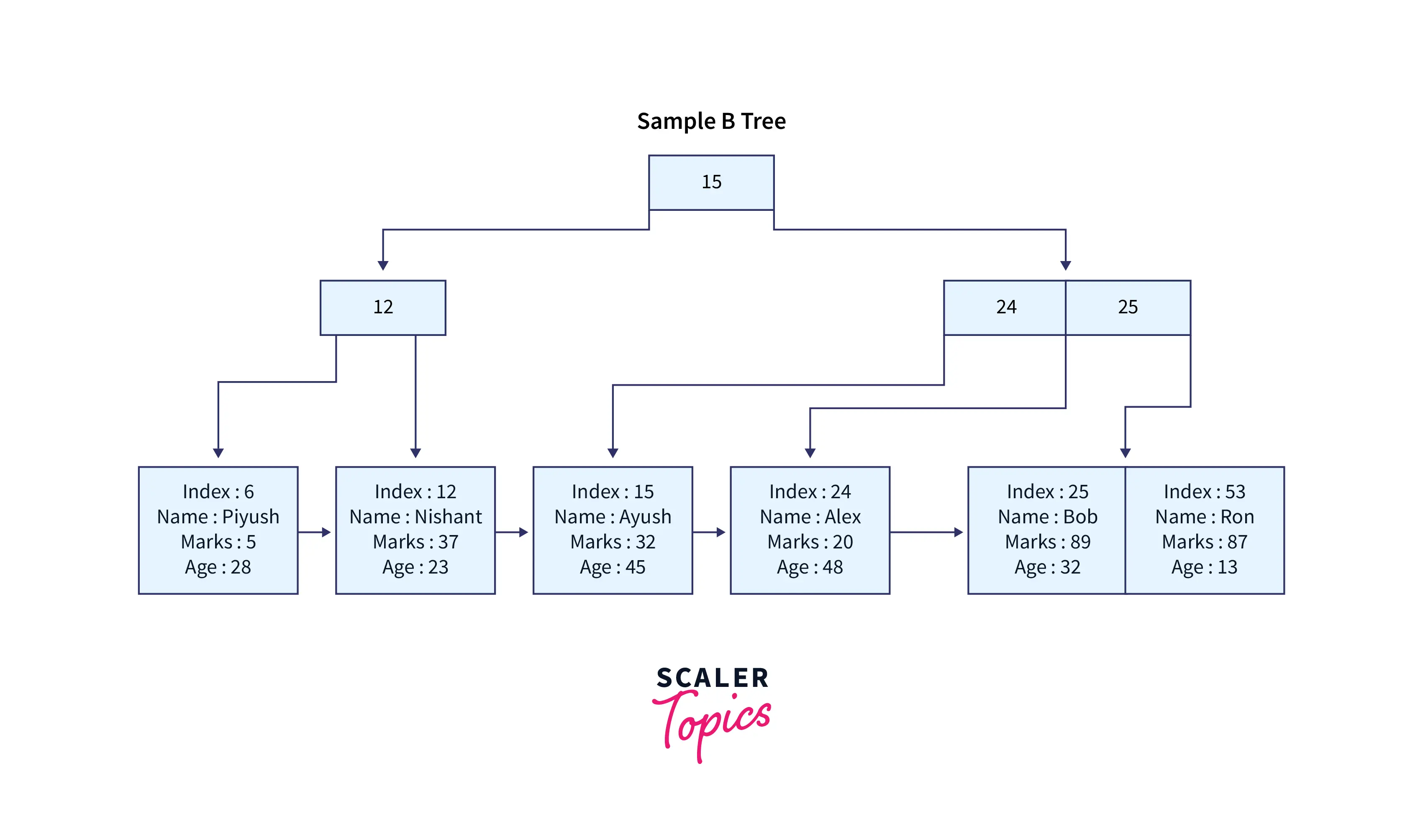
All records are kept in the leaf nodes of the B+tree, and the index is used as the key to create a B+tree. Non-leaf nodes do not store any records. Each leaf node contains a link to the next record in the tree. A database can do a binary search utilizing the index or a sequential search by merely traversing the leaf nodes to search through every entry.

If no indexing is utilized, the database will scan through each of these records to locate the provided record. The database builds three B-trees for each of the table's columns when indexing is enabled, as seen below. The key, in this case, is the B-tree key used for indexing. The index serves as a reference to the actual data record.

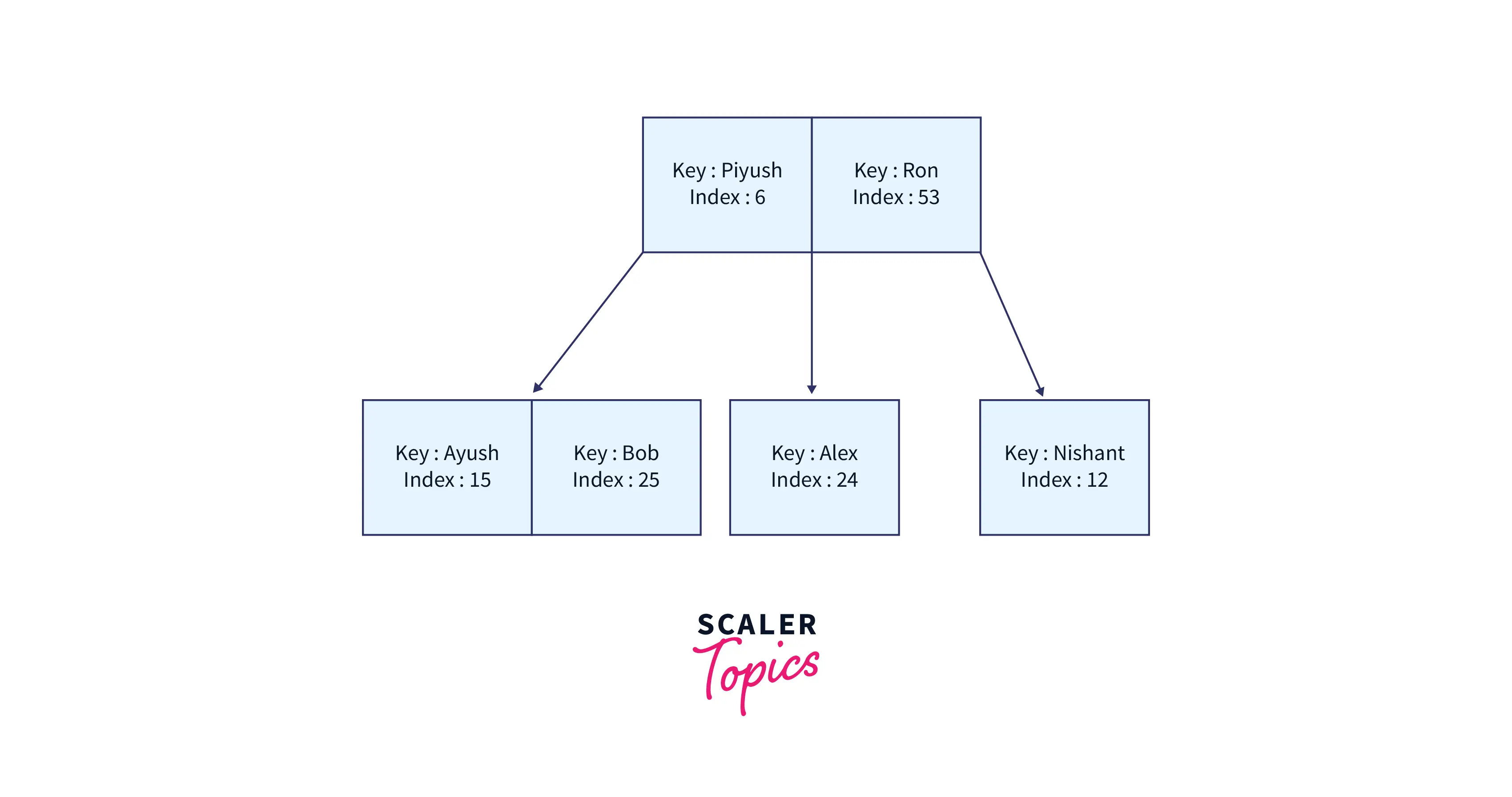
When indexing is utilized first, the database looks for a given key in the B-tree and returns the index in O(log(n)) time. Then, in O(log(n)) time, it runs another search in B+tree using the previously discovered index and obtains the record.

Each node in the B-tree and B+tree is stored within the Pages. The size of the pages is fixed. Pages are assigned a unique number beginning with one. A page number can be used to refer to another page. Page metadata such as the rightmost child page number, first free cell offset, and first cell offset are saved at the start of the page. A database can have two sorts of pages:

• Pages for indexing: These pages contain merely an index and a link to another page.
• Pages for storing records: These pages contain real data, which should be a leaf page.

Note: The B-tree allows the database to locate a leaf node quickly.

B Tree Traversal

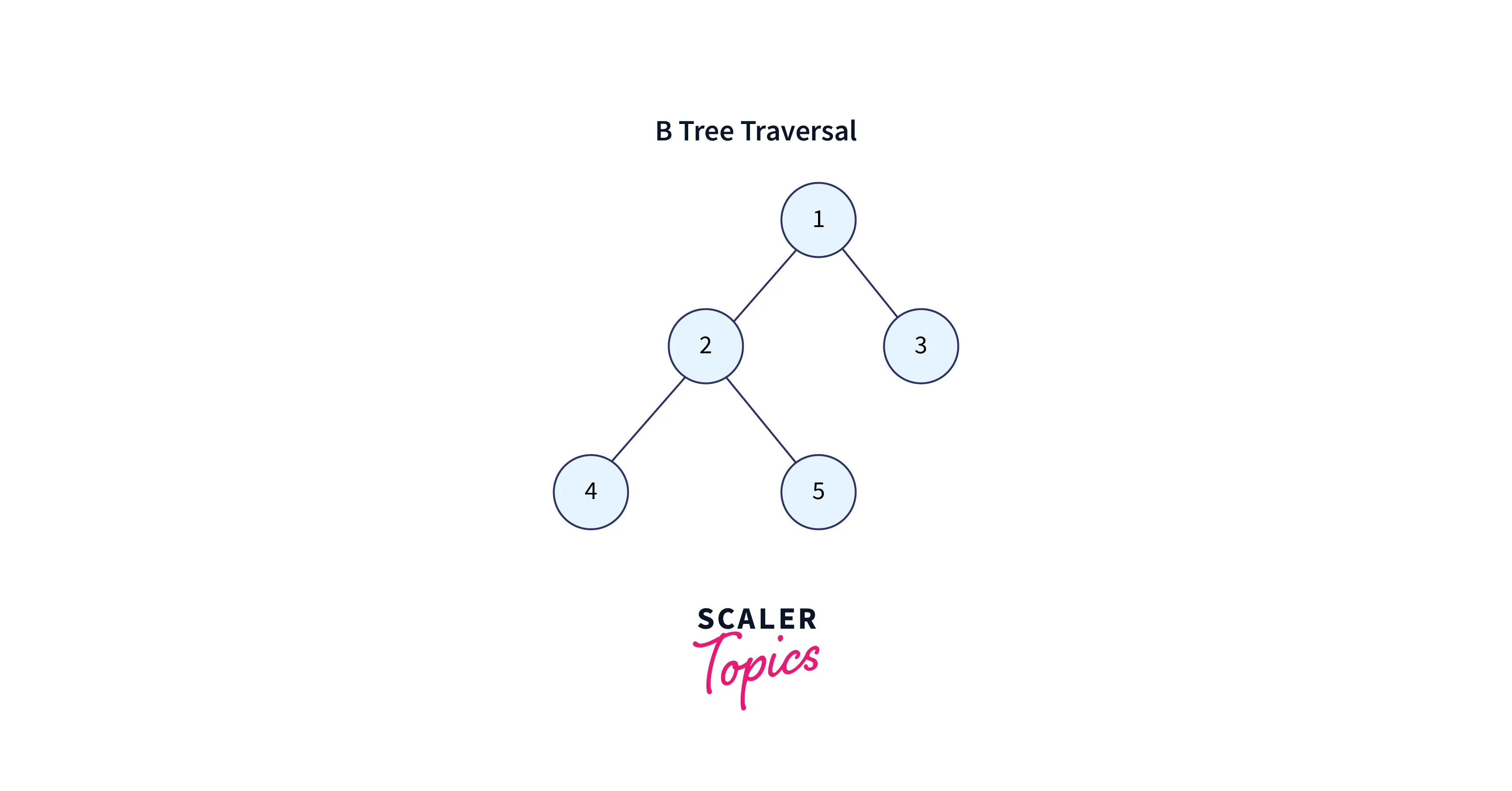
• Traversal is identical to Binary Tree Inorder Traversal. We begin with the leftmost child, print it recursively, and then repeat the operation for the other children and keys. Finally, display the rightmost child recursively.
• Each entry is processed in ascending order until a value exceeds or equals (>=) the search phrase. The database repeats the procedure until the tree traversal reaches a leaf node.
• The traversal of a tree is an extremely efficient process. Even on large data sets, it works almost instantly. This is due, first and foremost, to the tree balance, which provides access to all elements with the same amount of steps, and secondly, to the logarithmic increase of the tree depth. The tree depth develops very slowly in relation to the number of leaf nodes. Tree depths of four or five are common in real-world indexes containing millions of records. A tree depth of six is rare.

Reasons for Using B Tree Index in MySQL

1. When exploring tables on disc, the cost of accessing the disc is considerable, but the amount of data transferred is unimportant. As a result, we want to keep disc access to a minimum.
2. We understand that we won't be able to increase the height of trees. As a result, we want to keep the tree's height as low as feasible. We can use B-tree to solve this problem because it has more branches and so is shorter. Access time decreases as branching rises and depth decreases.
3. One node in a B-tree can hold multiple elements or things.

Let's create a clustered index for the LastName column now:

Let's now add a few more rows to the table:

The SELECT statement is as follows:

Take a look at how these rows currently appear on the B-Tree.

A data page is what the blue box represents (AKA a node). Data is stored in nodes like this on a hard disc. To store information, a hard disc has a TON of nodes.

It's not necessary to understand all of the inner workings of a data page/node, but it is necessary to understand that a node has a finite size. A node can only hold a certain number of rows.

Let's add a new row to our table.

The INSERT statement is as follows:

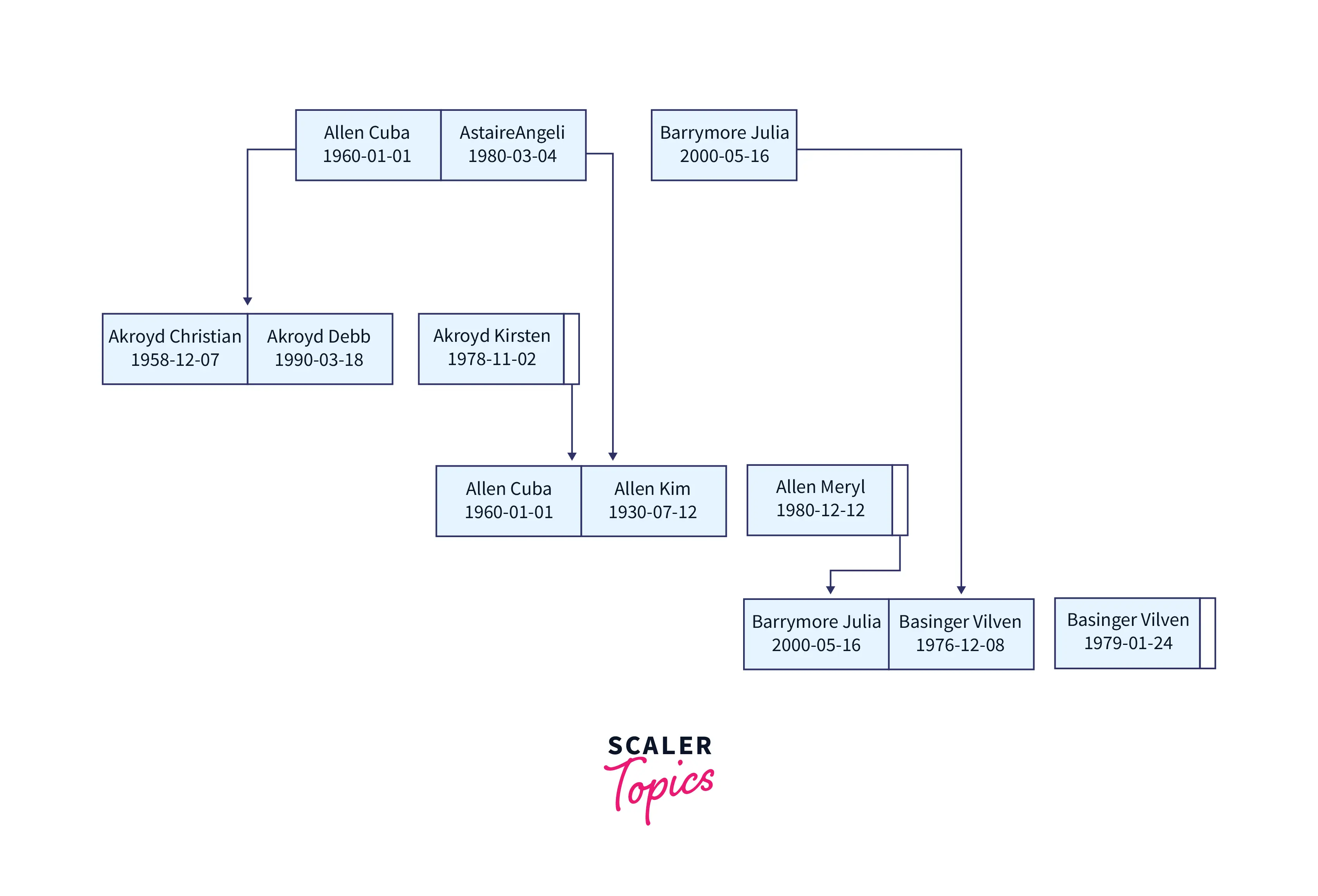
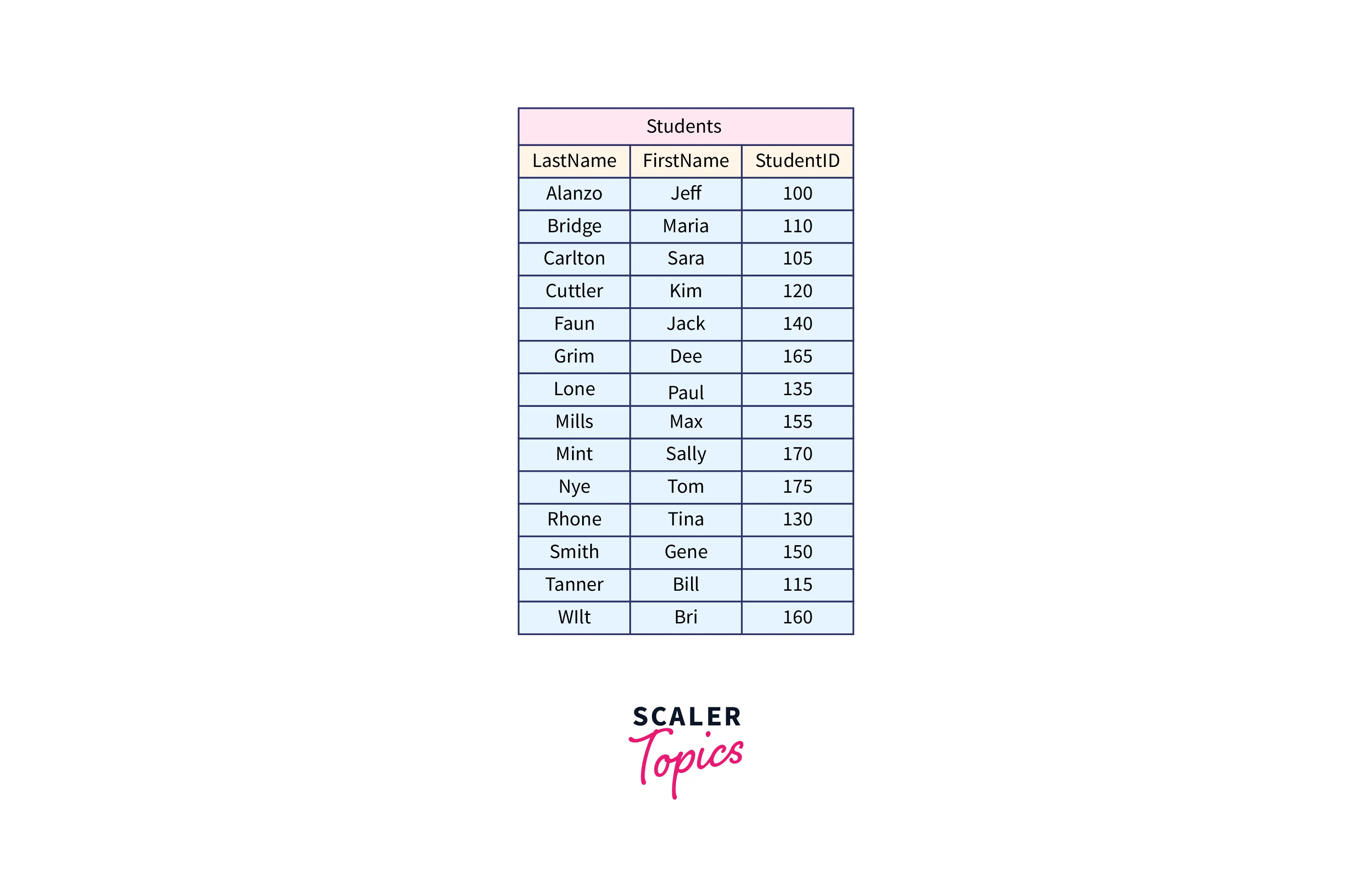
Our B tree should now look like this:

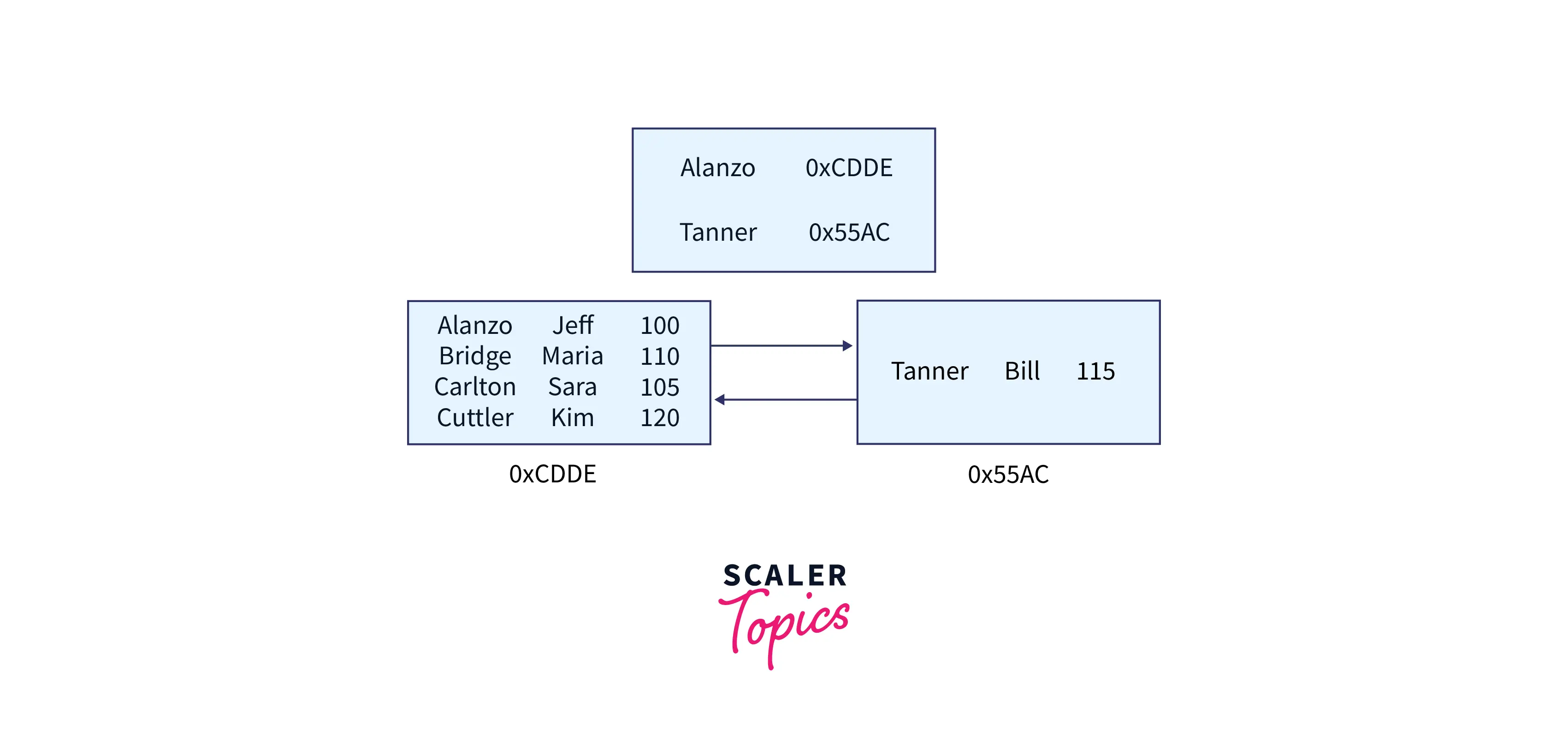
• The root node is the topmost node in the tree. The two nodes underneath are called leaf nodes. The real table data is stored in the leaf nodes (the LastName, FirstName, and StudentID all together).
• The strange alpha-numeric strings beneath each leaf node are the address of a leaf node.
• The two arrows between the two leaf nodes represent how the two leaf nodes are linked using a doubly-linked list. As a result, node 0xCDDE understands how to reach node 0x55AC, and node 0x55AC understands how to reach node 0xCDDE. They are connected to one another in both directions.
• All blue boxes are still known as nodes, and each node may only hold four objects.

Root node content

Let's discuss the root node's content. In the root node, each line carries two pieces of information:

1. The address of the leaf node to which it refers.
2. The leaf node to which it points has the smallest key value.

For example, the first line of the root node points to the node at address 0xCDDE. Alanzo is the node's minimal (or initial) key value.

To better clarify those two concepts, let's take a look at how SQL Server searches through this B-tree to find the information it needs. Assume we create the following query:

So basically, this query is looking for whatever we have for someone with the last name Carlton.

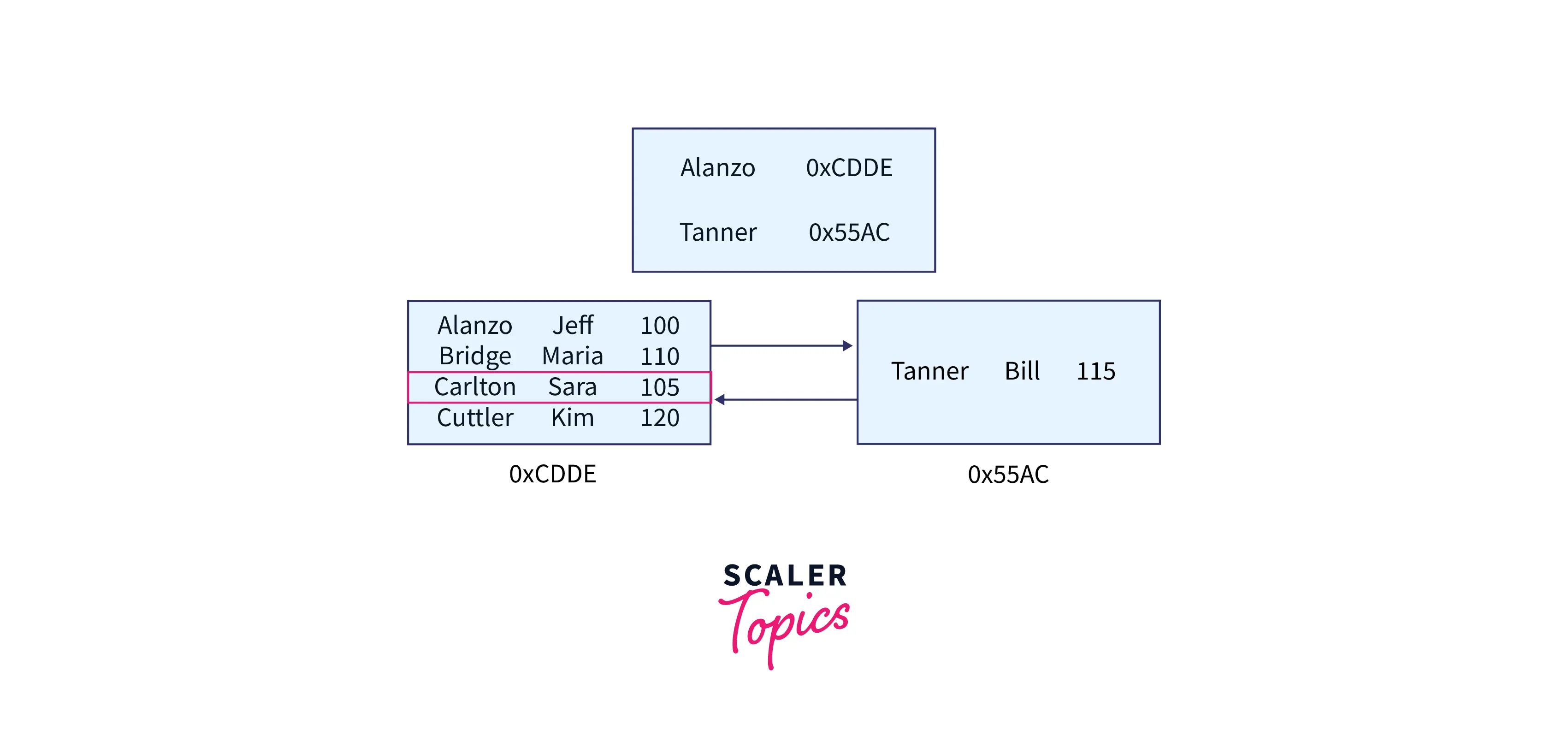
SQL Server will essentially traverse through the B-tree to find this information. It starts at the root node (the index's entry point) and goes through each key value. It stops searching the root node when it finds a key-value bigger than the key-value we're looking for.

For example, The first line in the root node has the key Alanzo, which is less than the key value we're seeking for (which is, once again, Carlton). So, because Alanzo is less than the desired value, SQL Server continues down the list.

Tanner is the next element in the root node list (this value is greater than the value we are seeking for).

As a result, SQL Server no longer searches through the root node. It now understands that the value we need must be found in a leaf node beginning with the name Alanzo.

Remember that each key value in the root node reflects the minimum key value of the leaf node it points to (Alphabetically, we know Alanzo could never come after Tanner).

We now know that we must search the node beginning with Alanzo. We need to know the node's address. The root node stores the address of any node beginning with Alanzo. It appears that the node beginning with Alanzo is located at 0xCDDE:

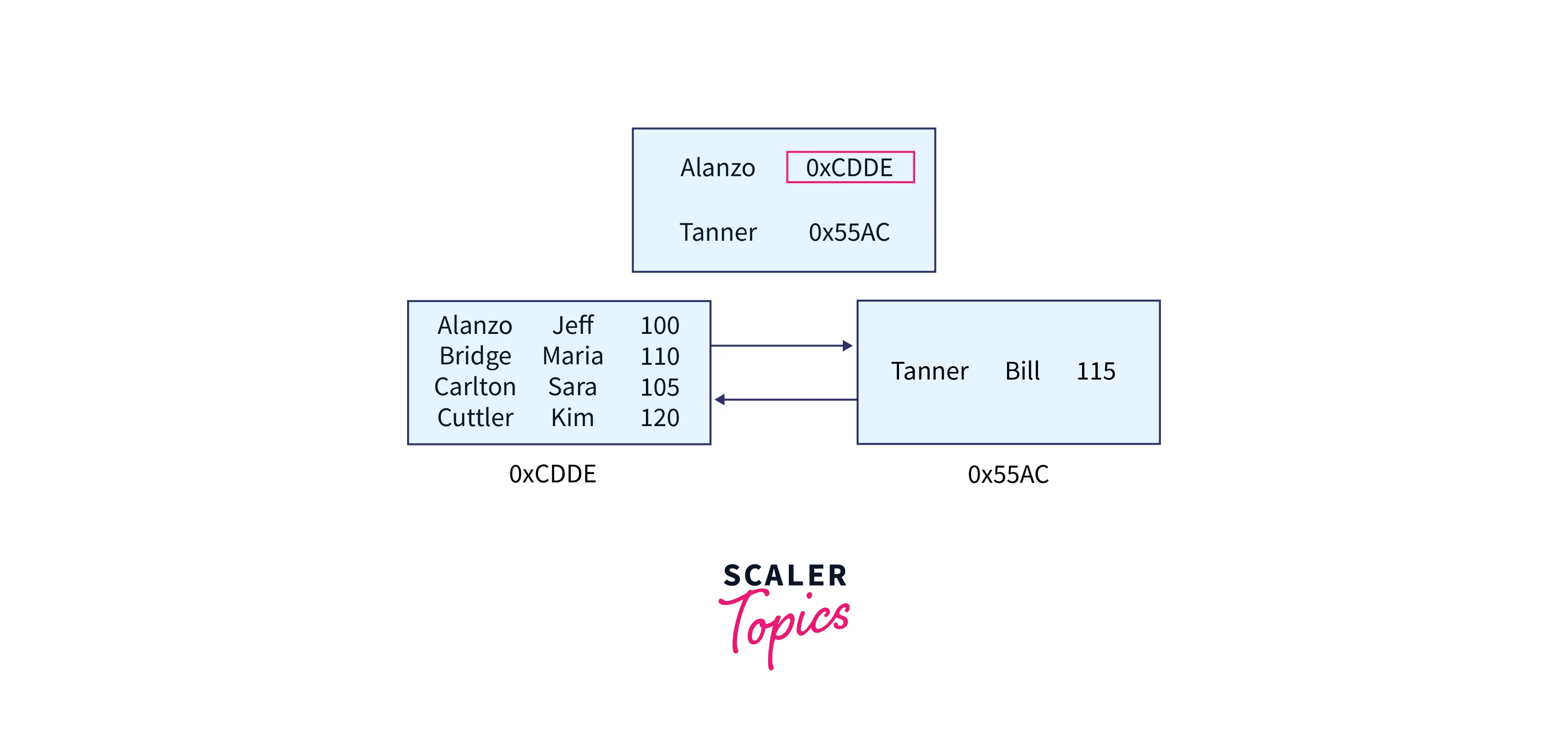
SQL Server understands where to proceed next: 0xCDDE is the address. It works along with the node's list of elements, beginning at the top until it finds the desired data.

Here's a great diagram that shows how SQL Server traverses the B-tree:

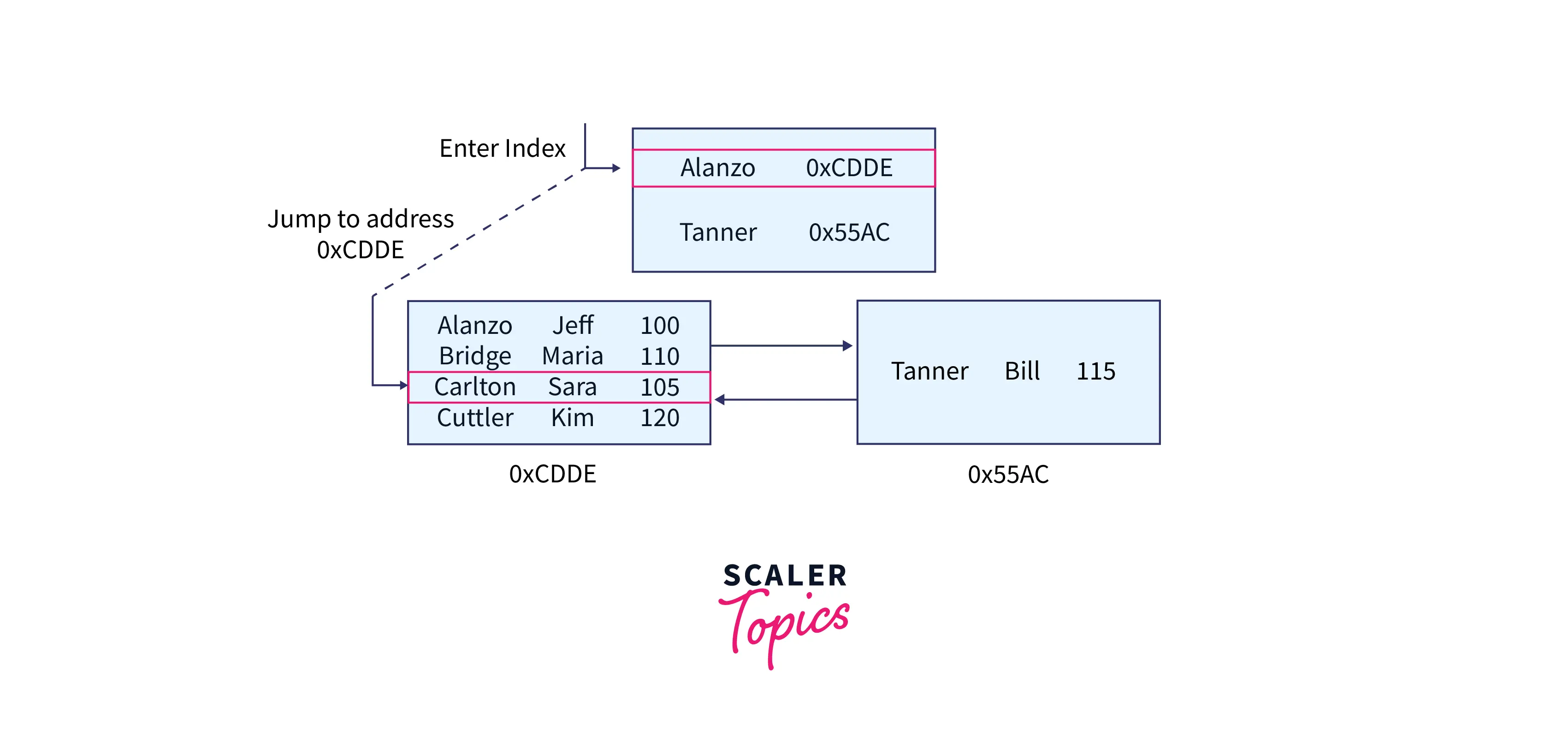
The stroll through the B-tree might be different if we were seeking for the last name Tanner instead.

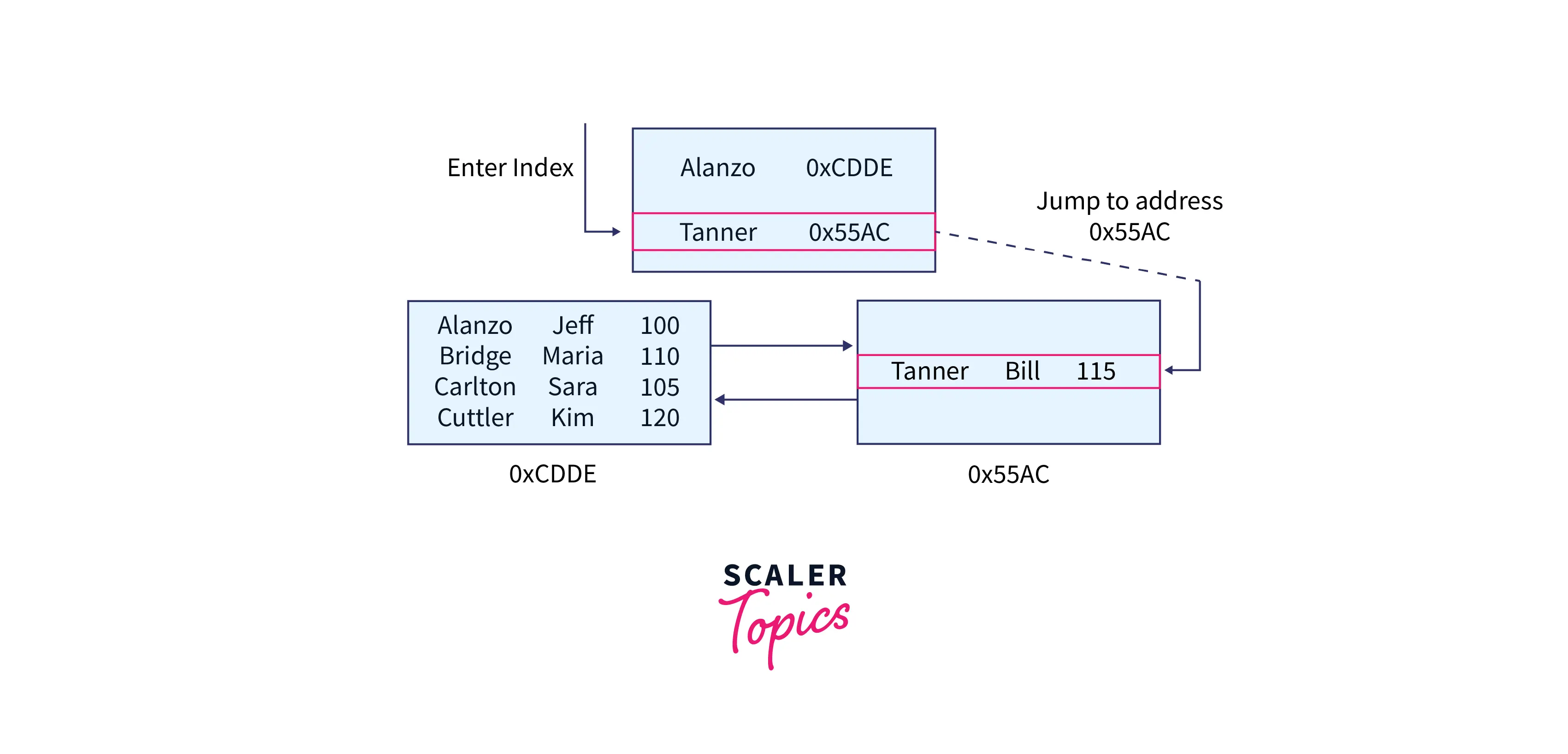
We still have one more scenario to go over. Let's add enough rows to our table to fill all of our nodes.

The INSERT statement is as follows:

Our B tree should now look like this:

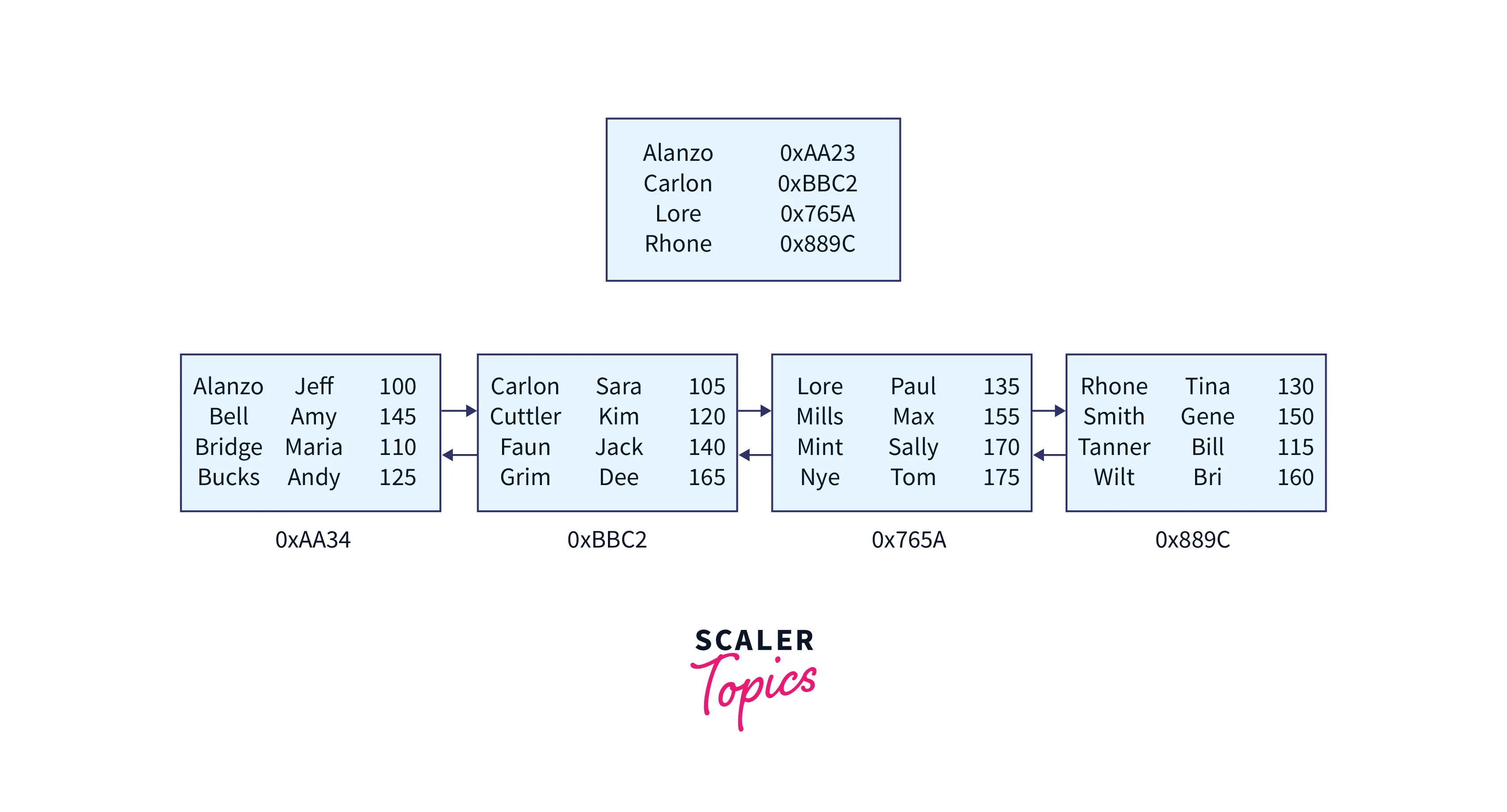
We've all been filled up, as you can see.

What happens if we wish to add another row?

Usually, if we wanted to add another row, we would simply create another leaf node and insert our new row data there. The issue is that there isn't enough room in the root node to refer to a new leaf node. The root node already contains four references, which is the maximum allowed!

Now, SQL will create another level, called an intermediate level.

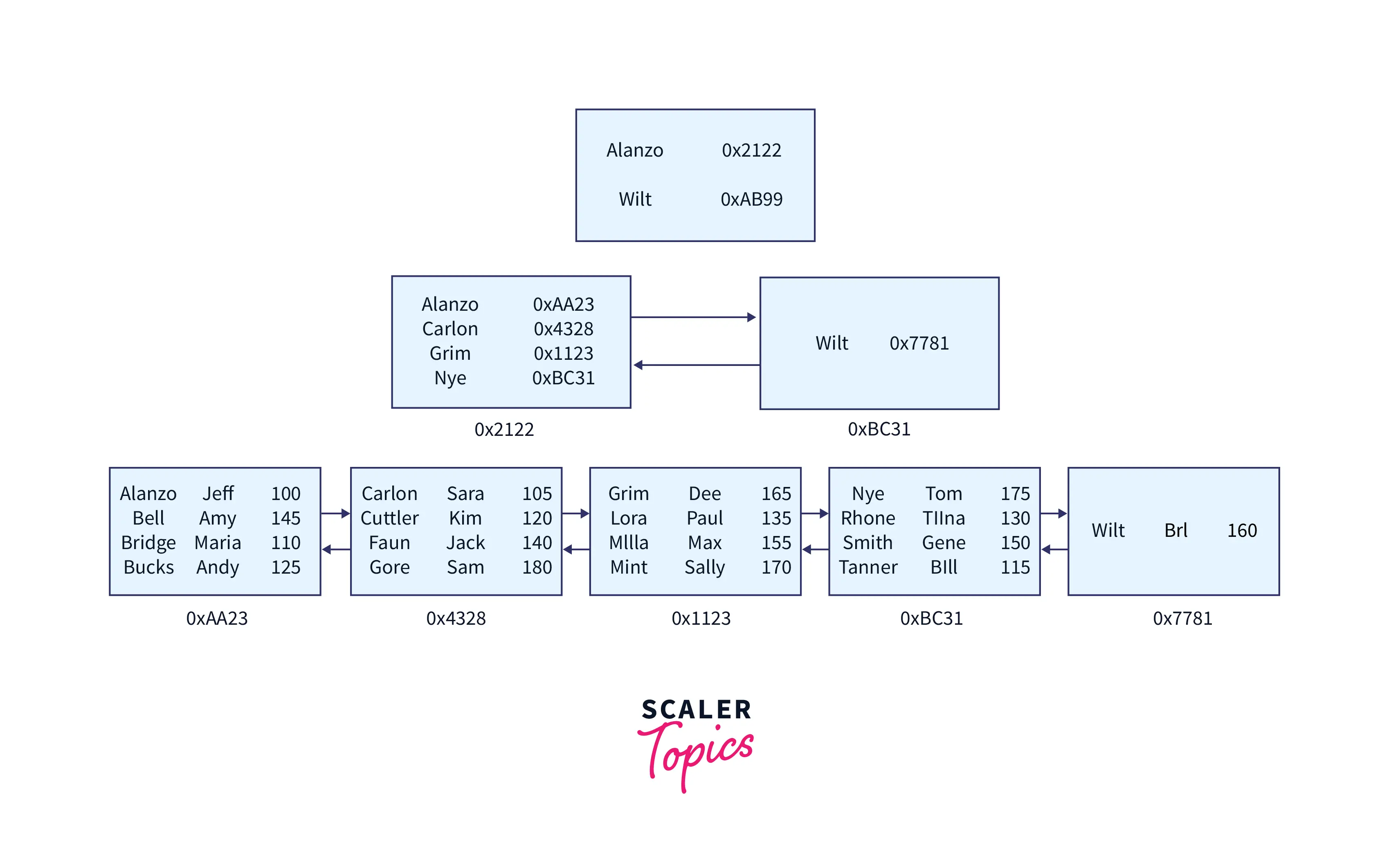
Let's start at the beginning with the root node. Every line in the root node still refers to another node. The reference, however, is now to an intermediary node.

The same rules apply as before. Each root node line contains two pieces of information:

1. The address of the intermediary node to which it points.
2. The minimal key value in the intermediate node it points to.

After then, each intermediary node functions as its own mini-root node. The rules for each line in the intermediate nodes are the same. Each intermediate node's line provides two bits of information:

1. The address of the leaf node to which it points.
2. The leaf node to which it points has the smallest key value.

This pattern continues as needed. Once all of the nodes in our B-tree have been filled, SQL Server will need to add another intermediate level to make additional room.