How to Find Standard Deviation in R?

What is Standard Deviation?

Standard deviation is a fundamental statistical concept used to quantify the variability or dispersion of data in a set. It provides valuable insights into the spread of values around the mean and is a powerful tool in analyzing and interpreting data. Understanding standard deviation is crucial in various fields, such as finance, science, economics, and social sciences, as it helps researchers, analysts, and decision-makers make informed judgments and draw meaningful conclusions.

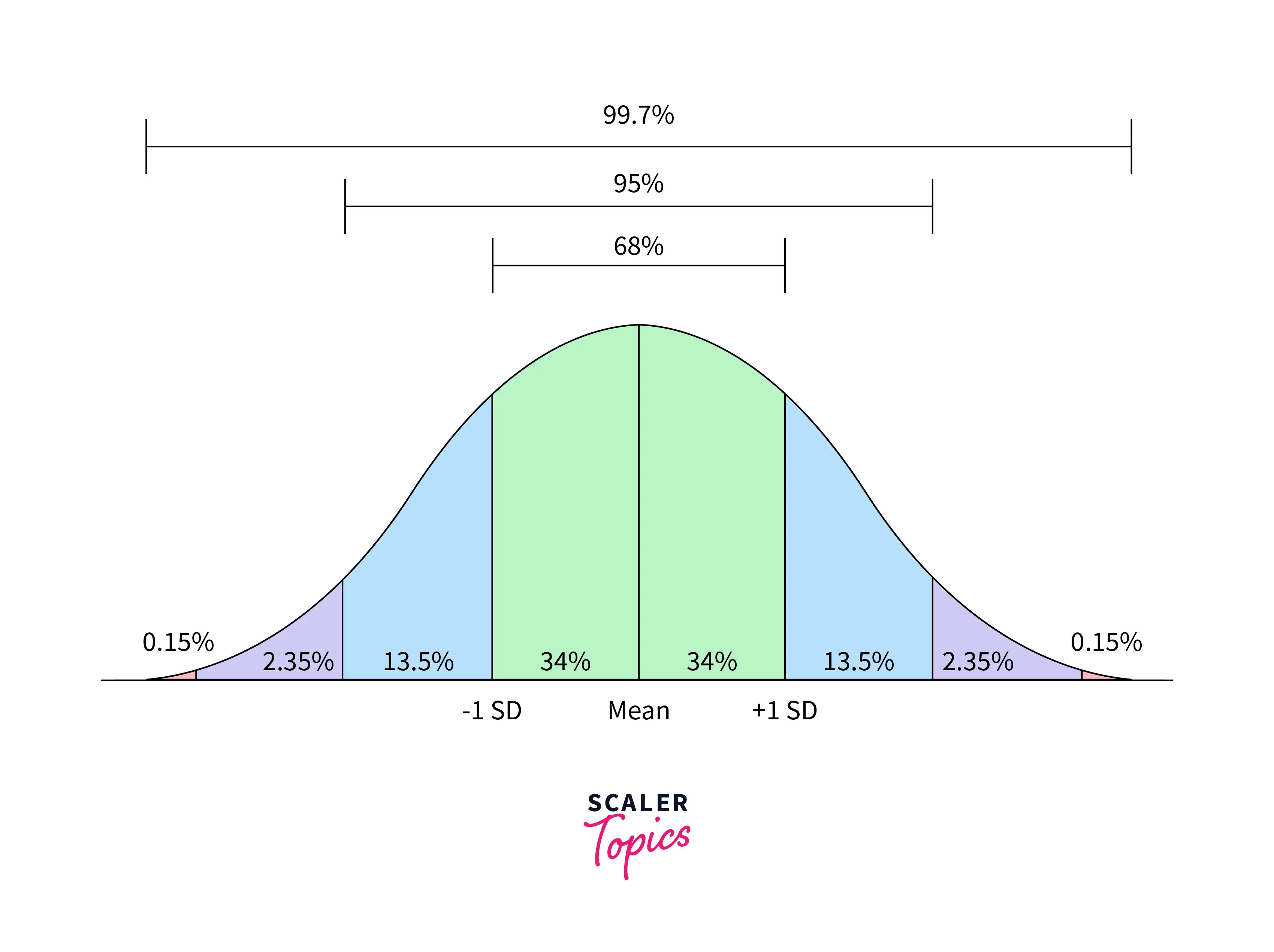
In a data set, individual values may deviate from the mean, either positively or negatively. The standard deviation measures the average amount by which these individual values differ from the mean. A larger standard deviation suggests that data points are more widely spread out, indicating greater variability, while a smaller standard deviation implies data points are closer to the mean, indicating lower variability.

Standard deviation helps identify outliers, which are data points far from the mean, and assess the reliability of the mean as a representative value for the data set. Additionally, when comparing two or more data sets, standard deviation aids in understanding which one has more consistent or homogeneous data.

The standard deviation is an essential tool in statistics as it allows you to understand the spread of data and make comparisons between different data sets. It is often used in various fields, including finance, science, economics, and social sciences.

Importance of Standard Deviation.

The importance of standard deviation lies in its ability to provide valuable information about the variability or dispersion of data in a set. Here are some key reasons why standard deviation is significant:

• Measure of Variability: Standard deviation quantifies the spread of data points around the mean. A higher standard deviation indicates a wider dispersion, while a lower standard deviation implies less variability. This information is crucial for understanding the distribution of data and the degree to which values deviate from the average.
• Assessing Data Quality: Standard deviation helps identify outliers and extreme values in the data set. Outliers can significantly impact the interpretation of results and influence statistical analyses. Detecting and handling outliers is essential to ensure data integrity and accuracy.
• Comparing Data Sets: Standard deviation enables comparisons between different data sets. When comparing the variability of two or more groups or populations, the one with a larger standard deviation will have more diverse data points, while the one with a smaller standard deviation will be more homogeneous.
• Risk Assessment: In finance and investing, standard deviation is used to measure risk. It provides an insight into the volatility of returns, helping investors understand the potential fluctuations in their investments. Higher standard deviation indicates higher risk, and lower standard deviation suggests a more stable investment.
• Decision-Making: Standard deviation aids in making informed decisions based on data analysis. For example, in manufacturing processes, monitoring standard deviation helps ensure consistency and quality. In social sciences, it allows researchers to draw conclusions about the significance of findings.
• Validating Hypotheses: When conducting experiments or studies, standard deviation helps researchers determine the reliability of results. It allows them to assess whether observed differences between groups are statistically significant or merely due to random chance.
• Quality Control: In various industries, standard deviation is used in quality control processes. It helps identify variations in production or performance, enabling companies to take corrective actions and improve processes.
• Predictive Modeling: Standard deviation plays a crucial role in predictive modeling and forecasting. It allows modelers to understand the uncertainty associated with predictions and estimate confidence intervals around forecasts.

Methods to Find Standard Deviation in R

In R, there are several methods to find the standard deviation of a dataset. Here are three common ways to calculate the standard deviation:

Using Standard Formula

Another way to calculate the standard deviation is to directly compute the sum of squared differences from the mean, divide it by the number of observations, and then take the square root. Here's how we can do it:

Let's go through each part of the code step by step:

• data <- c(10, 20, 15, 30, 25): This line creates a numeric vector named data containing the values 10, 20, 15, 30, and 25.
• mean_value <- mean(data): This line calculates the mean of the data vector using the mean() function in R which is the sum of all data points divided by the number of observations.
• squared_diff <- sum((data - mean_value)^2): This line calculates the sum of squared differences from the mean. It subtracts the mean value from each data point, squares the result, and then sums up all these squared differences. This is a crucial step in finding the variance.
• n <- length(data): It calculates the number of observations in the data vector using the length() function.
• variance <- squared_diff / (n - 1): It calculates the variance of the data vector. It divides the sum of squared differences from the mean by n - 1. The subtraction by 1 is for sample-based standard deviation. If you want to calculate the population standard deviation, you can use n instead of n - 1.
• standard_deviation <- sqrt(variance): This line calculates the standard deviation by taking the square root of the variance.
• print(standard_deviation): This line prints the calculated standard deviation to the console.

This manual approach is conceptually similar to using the sd() function, but it gives you more control over the intermediate steps and is helpful for educational purposes or if you need to understand the individual calculations involved in finding the standard deviation.

Using the sqrt() and var()

The standard deviation can also be calculated using the variance. The variance is the average of the squared differences from the mean. To get the standard deviation, you take the square root of the variance. Here's how you can do it:

Let's go through each part of the code step by step:

• data <- c(10, 20, 15, 30, 25): This line creates a numeric vector named data containing the values 10, 20, 15, 30, and 25.
• variance <- var(data): This line calculates the variance of the data vector using the var() function in R. Variance is a measure of how much the values in the dataset vary from the mean. It quantifies the average of the squared differences between each data point and the mean of the data.
• standard_deviation <- sqrt(variance): This line calculates the standard deviation by taking the square root of the variance. The standard deviation is the square root of the variance, and it represents the average amount of variation or dispersion of the data points from the mean. In other words, it tells us how much the individual data points deviate from the mean.
• print(standard_deviation): This line prints the calculated standard deviation to the console. The print() function is used to display the result of the calculation.

Putting it all together, the code takes the numeric vector data, calculates its variance using the var() function, then computes the standard deviation by taking the square root of the variance using the sqrt() function. Finally, it prints the result, which is the standard deviation of the data vector.

Using sd()

The sd() function in R calculates the standard deviation of a numeric vector or a data frame column. Here's the example:

This code calculates the standard deviation of the numeric vector data using the sd() function in R. Let's go through each part of the code:

• data <- c(10, 20, 15, 30, 25): This line creates a numeric vector named data containing the values 10, 20, 15, 30, and 25.
• standard_deviation <- sd(data): This line calculates the standard deviation of the data vector using the sd() function in R. The sd() function takes a numeric vector as input and returns its standard deviation. It uses a sample-based standard deviation formula by default (dividing by n - 1 instead of n), which is appropriate for a sample of data rather than an entire population.
• print(standard_deviation): This line prints the calculated standard deviation to the console. The print() function is used to display the result of the calculation.

The use of the sd() function is one of the most straightforward and convenient ways to find the standard deviation in R. It directly provides the result without requiring you to calculate variance separately.

Standard deviation for values in a list

To calculate the standard deviation for values in a list in R, you can follow similar steps as for a numeric vector. The only difference is that you need to access the elements within the list while performing calculations. Here's how you can do it:

Let's assume you have a list named data_list, and each element of the list contains a numeric vector with values:

Now, to calculate the standard deviation for each vector within the data_list, you can use a loop or one of the apply family functions. Here's an example using the sapply() function, which will apply the sd() function to each vector in the list and return the standard deviation values in a new vector:

This will output the standard deviation for each vector in the data_list.

Alternatively, you can also use a loop, such as a for loop, to calculate the standard deviation for each vector in the list:

Both methods will give you the standard deviation for each numeric vector within the list. The sapply() approach is more concise and often preferred for its simplicity, especially when working with large lists or data frames. However, the loop approach provides more flexibility and control if you need to perform additional operations on each vector within the list.

Standard Deviation for values in a CSV file

To calculate the standard deviation of values in a CSV file in R, you can use the read.csv function to read the data from the CSV file into a data frame and then use the sd function to calculate the standard deviation of the desired column(s) in the data frame. Here's how you can do it:

Assuming you have a CSV file named data.csv with the values you want to analyze, and you want to calculate the standard deviation of a specific column (let's say column 'ValueColumn'):

If you have multiple columns and want to calculate the standard deviation for each column separately, you can do so using the apply function:

In this case, the apply function is used to apply the sd function to each column of the data frame (excluding non-numeric columns) and returns a vector containing the standard deviation of each column.

High and Low Standard Deviation

A high and low standard deviation refer to the degree of variability or dispersion in a data set. Let's explore the characteristics of both scenarios.

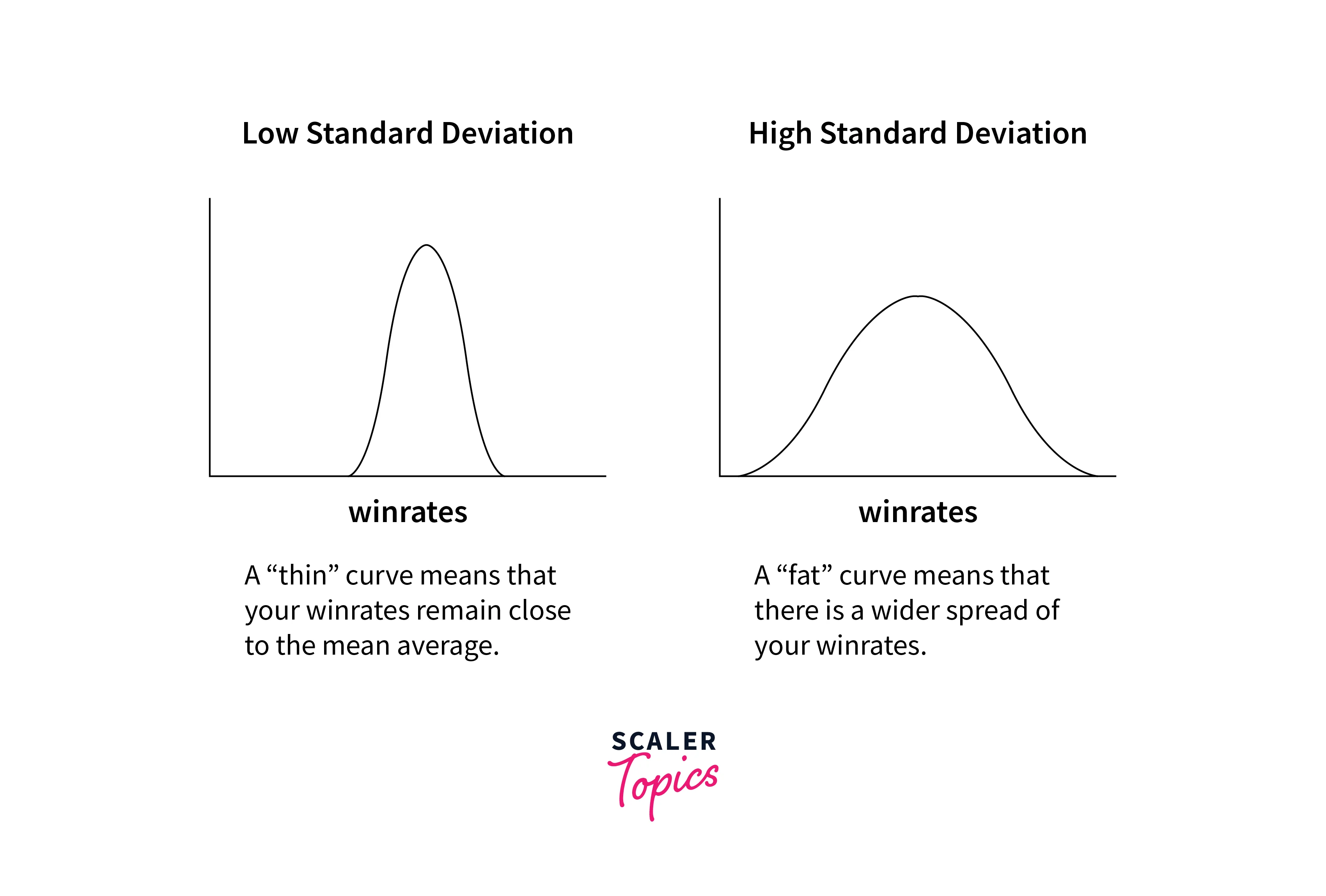
High Standard Deviation

• A high standard deviation indicates that the data points in the set are widely spread out from the mean.
• Data values are more diverse and have a broader range of values compared to the mean.
• The data points may be more spread out or scattered, making the distribution more spread.
• In terms of variability, a high standard deviation implies that individual data points deviate significantly from the mean, resulting in a less predictable pattern.
• High standard deviation is commonly associated with higher risk or uncertainty when making predictions or investment decisions.
• For example, in a financial context, a high standard deviation in investment returns suggests higher volatility, with greater potential for significant gains or losses.

Low Standard Deviation

• A low standard deviation indicates that the data points in the set are relatively close to the mean.
• Data values are more clustered around the mean, resulting in a narrower range of values compared to the mean.
• The data points are less spread out, making the distribution more concentrated or tightly packed.
• In terms of variability, a low standard deviation implies that individual data points deviate less from the mean, resulting in a more predictable pattern.
• Low standard deviation is commonly associated with lower risk or greater stability when making predictions or investment decisions.
• For example, in a financial context, a low standard deviation in investment returns suggests lower volatility, with less potential for significant gains or losses.

Overall, understanding whether a data set has a high or low standard deviation is crucial for data analysis, decision-making, and risk assessment. It helps researchers, analysts, and decision-makers interpret the data's characteristics and make informed judgments based on the level of variability present in the data.

Example 1 : Standard Deviation for a list of even numbers.

To calculate the standard deviation for a list of even numbers from 1 to 100 in R, you can create the list of even numbers first and then use the sd() function to calculate the standard deviation. Here's how you can do it:

Let's break down the code step by step:

• even_numbers <- seq(2, 100, by = 2): In this line, we use the seq() function to generate a sequence of numbers. The seq() function creates a sequence from the starting value (2 in this case) to the ending value (100 in this case) with a specified increment (by = 2 means we are generating only even numbers, as they are incremented by 2 in each step). So, even_numbers will be a numeric vector containing all the even numbers from 2 to 100, i.e., 2, 4, 6, 8, ..., 100.
• standard_deviation <- sd(even_numbers): Here, we use the sd() function to calculate the standard deviation of the even_numbers vector. The sd() function takes a numeric vector as input and returns the standard deviation of that vector.
• print(standard_deviation): Finally, we use the print() function to display the calculated standard deviation. The standard_deviation variable contains the result obtained from the sd() function, and using print() will output the value to the console.

When we run the code, it generates the list of even numbers from 1 to 100, calculates the standard deviation for that list, and prints the result.

Example 2 : Standard Deviation for US population data.

To calculate the Standard Deviation of US Population Data we need to download the excel file from this link . To install and load the readxl package which read data from an Excel file, and then calculate the standard deviation for a specific row in the dataset. It's important to note that the specific row number (255 in this case) might vary depending on the dataset.

Let's go through the steps and make sure everything works as expected:

Install and load the 'readxl' package (if you haven't already done so). You only need to install the package once; loading it is sufficient for future sessions.

Read the Excel data into the data variable. Make sure the file path is correct. Since the file extension is .xls, the read_excel function should be used. If the file extension is .xlsx, you would use read_xlsx.

Select the specific row corresponding to the USA data and calculate the standard deviation.

Ensure that the file path is correct and that you have the readxl package installed. After running the code, we should get the standard deviation of the USA data in the selected row printed on the screen.