Sum of First N Natural Numbers

Pseudo Code

Think intuitively, about how you can get the sum of the first N natural numbers iteratively! Here are the steps we'll follow:

• We will take the input of N from the user.
• We will use a sum variable which will store our desired sum, and set it to zero initially.
• We shall iterate from 1 to N, using another variable (let's say i). At each step, we shall add i to our sum variable.
• When we reach N (i.e $i == N$), the resultant sum will be our answer.

Let us now see the pseudo-code for the above:

1. int N, sum = 0, i = 1
2. Input N from user
3. do
4. sum = sum + i
5. i = i + 1
6. Repeat step 3 to 5 till $i <= N$
7. Display the value of sum

8 Methods to Find Sum of First N natural Numbers

Let us now see the various methods to find the sum of first N natural numbers.

Sum of Natural Numbers Using for Loop

Now we'll see the steps and code in C for calculating the sum of first N natural Numbers using for loop.

Steps:

• We will take the input of N from the user.
• We will initialize a sum variable to zero.
• We shall iterate from 1 to N, using another variable (let's say i). The for loop shall run from i = 1 until i is less than equal to N. After each iteration, we will increase i by 1 inside the conditional iterative statement of for loop.
• We shall keep on adding i to our sum as long as the for loop runs.
• When we come out of the for loop, it implies i has already reached N. Thus we will print our sum.

Code:

Input/Output:

In the above example, the loop is iterated 5 times and the value of i has been added to the sum each time. If our for loop runs N times, the number of operations performed inside the loop is N. Thus the time complexity used for loop here is $O(N)$. Since we aren't using any extra space, the space complexity is $O(1)$.

Sum of Natural Numbers Using While Loop

Let us see the steps and code in C for calculating the sum of first N natural Numbers using a while loop.

Steps:

• We will take the input of N from the user.
• We will initialize a sum variable to zero.
• We shall iterate from 1 to N, using another variable (let's say i). Outside the while loop, we will initialize i as 1. The while loop will run until i is less than equal to N. We will keep on increasing the value of i by 1 in each step.
• We shall keep on adding i to our sum as long as the while loop runs.
• When we come out of the while loop, it implies i has already reached N. Thus we will print our sum.

Input/Output:

In the above example, the loop is iterated 5 times and the value of i has been added to $sum$ each time. If our while loop runs N times, the number of operations performed inside the loop is N. Thus the time complexity using While loop here is $O(N)$. Since we aren't using any extra space, the pace complexity is $O(1)$.

Sum of Natural Numbers Using do-while Loop

The steps involving calculating the sum of the first N natural numbers using a do-while loop are similar to the while loop. The only difference is that this loop will execute the code block at least once, before checking if the condition is true. Then it will repeat the loop as long as the condition is true.

Let us see how the do-while loop works while calculating the sum of N natural numbers using the example below:

Let N = 5

• Initially i will be set to 1 and sum will be set to 0.
• After the first step sum will be 0+1 = 1 and i will be 2, and since 2 is lesser than 5, the loop will continue.
• After the second step sum will be 1+2 = 3 and i will be 3, and since 3 is lesser than 5, the loop will continue.
• After the third step sum will be 3+3 = 6 and i will be 4, and since 4 is lesser than 5, the loop will continue.
• After the fourth step sum will be 6+4 = 10 and i will be 5, and since 5 is equal to 5, the loop will continue.
• After the fifth step sum will be 10+5 = 15 and i will be 6, and since 6 is equal to 5, the loop will break, and we will print 15 to the screen.

Input/Output:

As you can see, the addition process (sum = sum + i) is running N times, and each time it is checked if i is less than equal to N. It will stop after N time, because i will no longer be less than equal to N.

Thus, using a do-while loop the time complexity is $O(N)$. Since we aren't using any extra space, the space complexity is $O(1)$.

Sum of Natural Numbers Using the Mathematical Formula

The sum of first N natural numbers can be calculated directly with the following mathematical formula: $1 + 2 + 3 + ... + N-2 + N-1 + N = N*(N+1)/2$

The above formula can be proved through the Principle of Mathematical Induction.

Let's see it with the following code:

Input/Output:

Since the $sum$ is calculated directly using the above formula, only one operation is occurring to obtain our desired result. Thus the time complexity is $O(1)$. We aren't using any extra space here, which is why our space complexity is $O(1)$.

Sum of Natural Numbers Using Function

We can keep a separate function to take a value N and calculate the sum of the first N natural numbers. That function will be called from main with the value of N as inputted by the user. The working of the function can be implemented using any of the methods discussed above.

Steps:

• We will take the input of N from the user.
• We call our function for calculating the sum and pass the value of N to it.
• Inside our function, a loop shall run from 1 to N, using another variable (let's say i). The for loop shall run from i = 1 until i is less than equal to N. After each iteration, we will increase i by 1 inside the conditional iterative statement of for loop.
• We shall keep on adding i to our sum as long as the for loop runs.
• When we come out of the for loop, it implies i has already reached N. Thus we will return our sum.
• We will update our sum variable inside our main function by storing the return value from the above function.
• The sum will be printed to the screen.

Input/Output:

Inside the above function, the loop is iterated 5 times and the value of i has been added to sum each time. The sum is then returned to the main function and displayed on the screen.
The time complexity is the same as the time complexity of the function. We are using for loop in our function, and we already saw that using for loop, N operations are performed to calculate the sum of the first N natural numbers. Thus, the time complexity is $O(N)$. Since we aren't using any extra space, our space complexity is $O(1)$.

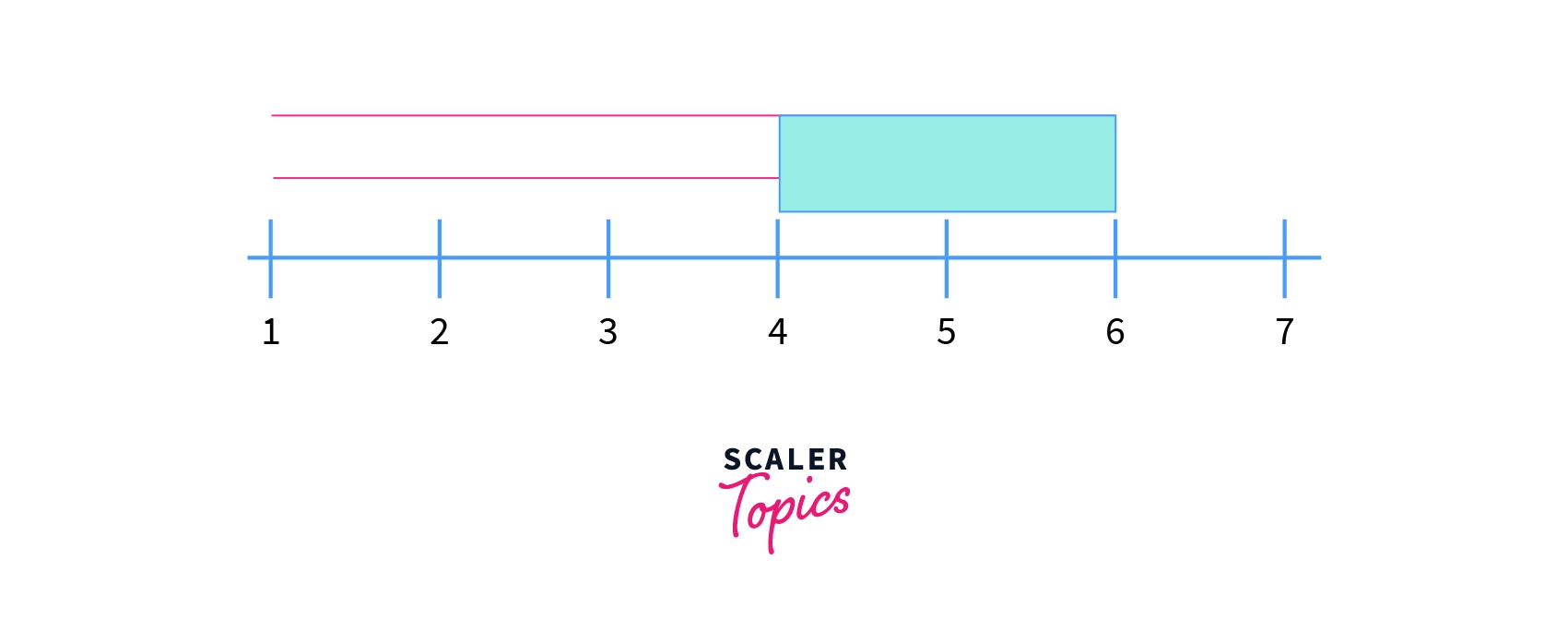
Sum of N Natural Numbers Between a Given Range

Sum of natural numbers between a given range say, N1 and N2, where $N1 < N2 = Sum$ of natural numbers from 1 to $N2 - Sum$ of natural numbers from 1 to $(N1 - 1)$.

Let us understand this with the below example:
N1 = 4
N2 = 6
Required Sum = 4 + 5 + 6 = 15
Sum of natural numbers from

1 to 6 = 6*(6+1)/2 = 21 ---(i)
Sum of natural numbers from

1 to 3 = 3*(3+1)/2 = 6 ---(ii)

Now, subtracting (ii) from (i), we get, 21 - 6 = 15, which is also equal to our desired sum! This is represented by the shaded portion of the figure below:

Let us now see the steps and code for the above logic.

Steps:

1. Like the previous method, we keep a function that will return to us the sum of the first N natural numbers.
2. We take the input of N1 and N2 from our user.
3. We pass N1 - 1 to our above function and get the sum of natural numbers from 1 to N1 - 1, let's call it sum1.
4. We pass N2 to our above function and get the sum of natural numbers from 1 to N2, let's call it sum2.
5. We display sum2 - sum1 on our screen.

Input/Output:

Inside the above function, the loop is iterated 3 times (N1 - 1) once, and 5 times(N2) next. Thus this is a linear-time operation. The time complexity is $O(N)$ and space complexity is $O(1)$.

Sum of n natural numbers Using Recursion

How would you calculate the sum of n natural numbers, if you were given the sum of n-1 natural numbers?

You would add n to it!

Therefore, mathematically:

Sum(N) = Sum(N-1) + N
Sum (N-1) = Sum(N-2) + (N-1)
Sum(N-2) = Sum(N-3) + (N-2)
.
.
.
Sum(1) = Sum(0) + 1
Sum(0) = 0

This is the intuition behind our recursive solution. For a given N, our recursive function will assume we have the sum of the first N-1 natural numbers, and then add N to it. Then our function will be recursively called for N-1, N-2, and so on until our N is 0.

Input/Output:

Let us understand how our recursive function will calculate the sum of first 5 natural numbers:

Sum = 5 + Sum(4);
Sum = 5 + 4 + Sum(3);
Sum = 5 + 4 + 3 + Sum(2);
Sum = 5 + 4 + 3 + 2 + Sum(1);
Sum = 5 + 4 + 3 + 2 + 1 + Sum(0);
Hence, Sum = 5 + 4 + 3 + 2 + 1 + 0 = 15;

Thus time complexity is $O(N)$. The space complexity is $O(N)$ since a recursive solution will be using the recursive call stack shown above.

Sum of n natural numbers Using an Array

We can also use an array to store the sum of n natural numbers. This approach is not recommended since we have more efficient solutions, which do not require an auxiliary space.

Input/Output:

The time complexity for inserting the elements in the array is $O(N)$ and for traversing the array to calculate the sum is $O(N)$. Thus overall time complexity is $O(N)$. The space complexity is $O(N)$ since we are using auxiliary space, which is, an array of size N.

See Also

• Find sum of the first n even natural numbers