sunny Number in Java

A number N is said to be a sunny number if (N+1) is a perfect square. This also implies that a sunny number in Java exists for all the perfect squares. For a perfect square P, (P-1) is a sunny number. There are many sunny numbers present in our number system.

Sunny number in Java help us identify patterns and build relationships within the realm of numbers and mathematics. They encourage problem-solving and critical thinking skills.

Sunny number in Java Example

Let us take an example of sunny numbers in Java.

Example 1 INPUT: 9 OUTPUT: No EXPLANATION: (9 + 1) = 10, we know that 10 is not a perfect square.

Example 2 INPUT: 743043 OUTPUT: Yes EXPLANATION: (862 * 862) = 743044 is a perfect square and therefore, 743043 is a sunny number.

Example 3 INPUT: 47 OUTPUT: No EXPLANATION: (47 + 1) = 48, we know that 48 is not a perfect square.

Example 4 INPUT: 0 OUTPUT: Yes EXPLANATION: (0 + 1) = 1, we know that 1 * 1 = 1, 0 is a sunny number.

Example 4 INPUT: -145 OUTPUT: No EXPLANATION: The square of any number is going to be positive. 0 is the smallest square and therefore -1 is the smallest sunny number.

How to Check sunny number in Java?

So we know that if the given number N is a sunny number (N+1) is a perfect square. A perfect square is a number whose square root is a whole number. For example, 9 is a perfect square as the square root of 9 is 3 i.e. 3*3=9. Similarly, 225 is a perfect square as 15*15=225.

The simplest approach we can think of to find whether the given number is a sunny number in Java or not is:

• Add 1 to the given number.
• Check if the resultant number is a perfect square.

To check if a number is a perfect square or not in Java, there are several ways:

• Firstly, we can use a built-in Math libraries method Math.sqrt().
  • It returns a double value. This double value can be simply rounded off.
  • The integer value is then multiplied by itself to get the square. This square is then compared with our resultant. If these are equal then the given number is a sunny number.
  • Let us see examples to understand this approach:
    • For the value of N = 44, we will add one to it thus resultant value is 45 now. The square root of 45 = 6.71. This will be rounded to 7. We know that the square of 7 is 49 which is not equal to 45 and thus N is not a sunny number.
    • Let us say N = 63. The resultant number will be 64. On using the Math.sqrt() function we will get 8.0 which will be rounded to 8. The square of 8 will equal to 64 and thus, 63 is a sunny number.
    • We will check the
• The second method uses the binary search.

  • Binary search is a searching algorithm used in cases where we have the lower bound and upper bound known as search space, a condition to discard the values from the search space and a target we are looking for.

  • Binary search helps us find the value in log(N) time complexity where N is the number whose square root we are looking for.

  • We can have a lower bound as 0 and an upper bound as N as the square root is always less than or equal to N.

  • In each iteration, we can find the mid value by taking an average of lower and upper bounds.

  • This mid value is multiplied by itself to get its square. This square is compared with the target square.

  • If the target is less than the square of mid, the result is not beyond mid or equal to mid. Therefore, we can reduce our search space by making upper bound as mid - 1

  • Similarly, if the target is greater than the square of mid, then we can discard checking all the numbers less than mid along with mid by making the lower bound as mid+1.

  • Else, the square of the mid is equal to the target. Thus, the target is the perfect square and our N is a sunny number.

  • Say, for example, our N = 8.

  • N + 1 = 8 + 1 = 9

  • Let us prove using a binary search that 9 is a perfect square.

  • Iteration 1:

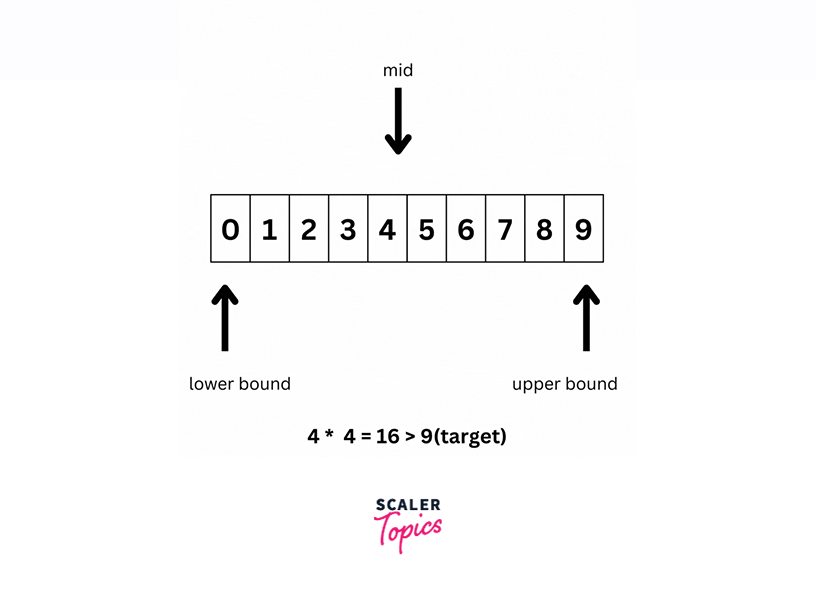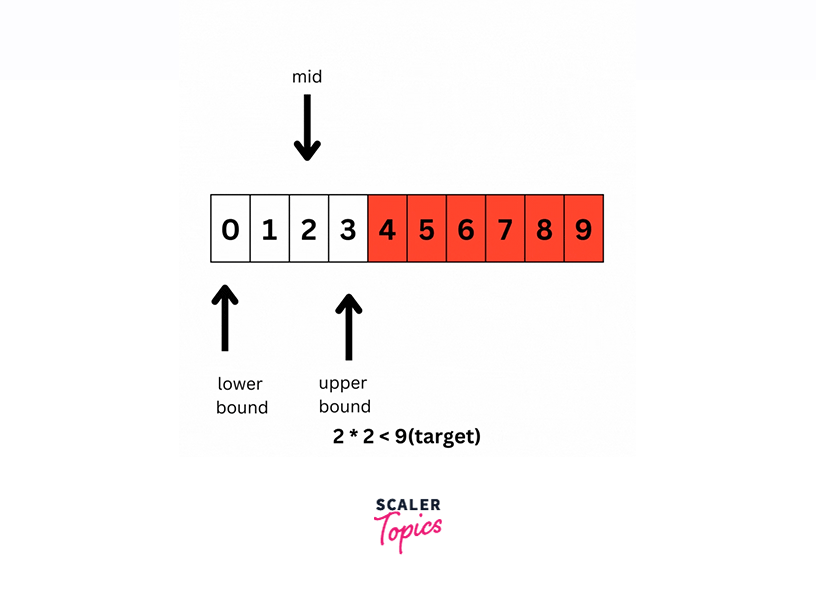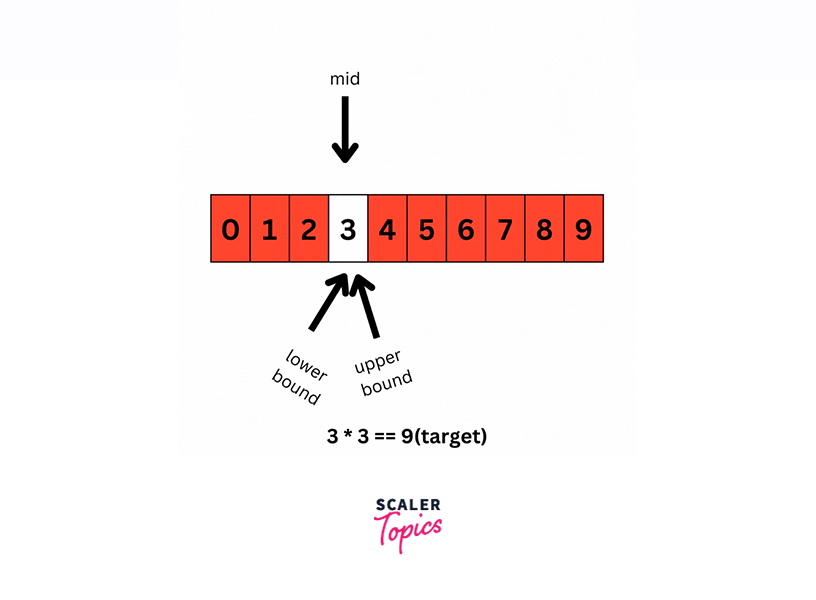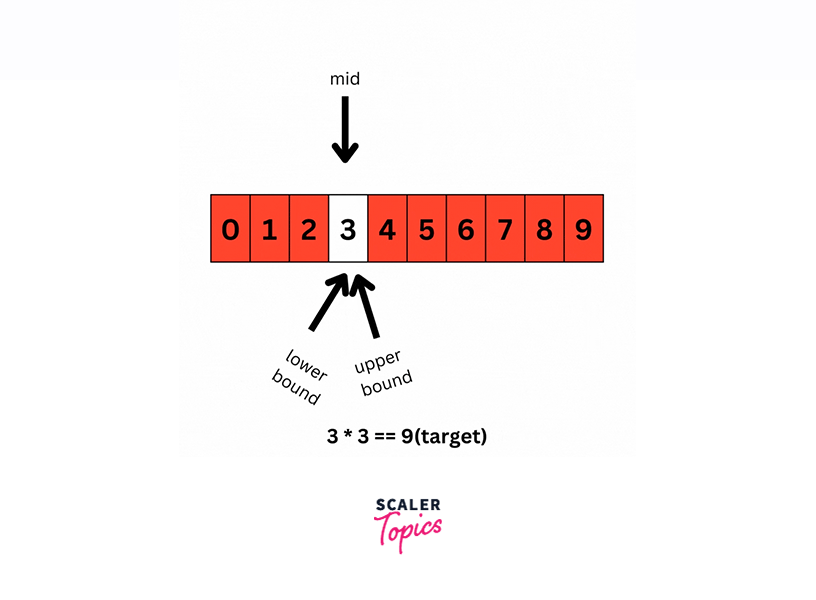
    • Lower bound: 0

    • Upper bound: 9 (N + 1)

    • Mid value: 4 (average of lower and upper bounds)

    • Mid square: 16 (4 * 4)

    • Comparison: 16 is greater than 9 (target)

    • Action: Set the upper bound to mid - 1, which becomes 3.

    • Here, the square of any number greater than 4 or 4 itself is not going to be less than or equal to 9. Therefore we can change our lower bound to 3.

    • Iteration 2:

    • Lower bound: 0

    • Upper bound: 3

    • Mid value: 2 (average of lower and upper bounds)

    • Mid square: 4 (2 * 2)

    • Comparison: 4 is less than 9

    • Again we know that if a < b, then a^2 < b^2. Therefore, we can reduce the search space by discarding anything that is on the left of 2.

    • Iteration 2:

    • Lower bound: 3
    • Upper bound: 3
    • Mid value: 3 (average of lower and upper bounds)
    • Mid square: 9 (3 * 3)
    • Comparison: 9 is equal to our target

  • Action: Square root found! 9 is a perfect square; therefore, 8 is a sunny number.

    

sunny Number in Java Program

Using Math.sqrt() method

Time complexity refers to the amount of time consumed by the program to complete its execution. Similarly, space complexity is the amount of space required.

The Math.sqrt() method and all the other calculations are done in constant time complexity irrespective of the size of the number. Also, no extra space is used in this program and therefore we can say that it occupies constant space.

Time Complexity: O(1)

Space Complexity: O(1)

Using binary search

Binary search is not an ideal solution but is a good way to practice binary search. It takes O(log n) time complexity to search for the number where n is the number. Again, we are not using any space.

Time Complexity: O(log n)

Space Complexity: O(1)