Support Vector Regression in Machine Learning

In machine learning, regression and classification are two fundamental tasks. While regression predicts continuous outcomes, classification categorizes inputs into classes. This article elucidates the disparities between regression and classification methodologies, focusing on Support Vector Machines (SVM) and Support Vector Regression (SVR).

Support Vector Machine (SVM)

Support Vector Machine (SVM) is a powerful supervised learning algorithm used for both classification and regression tasks. At its core, SVM aims to find the optimal hyperplane that separates different classes in a dataset, maximizing the margin between classes. This hyperplane serves as the decision boundary, allowing SVM to effectively classify new data points based on which side of the hyperplane they fall on. SVM is particularly effective in high-dimensional spaces and is capable of handling both linear and non-linear classification tasks through the use of various kernel functions. Its versatility and robustness make it a popular choice in a wide range of applications, including image classification, text categorization, and bioinformatics.

Let us understand SVM with an example. Let's say we have below classes plotted on a graph:

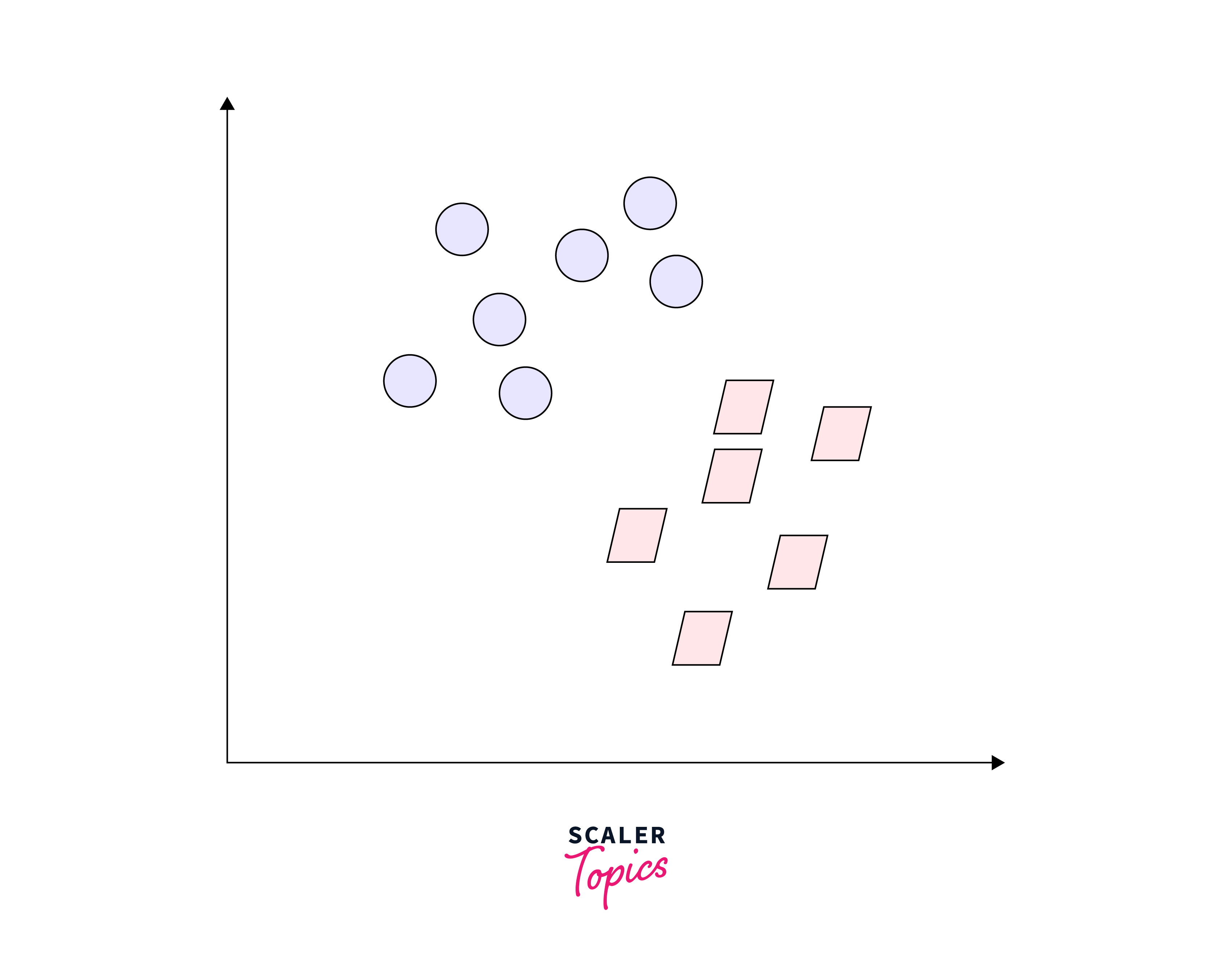
Could you determine what the dividing line should be? You might have thought of something like this:

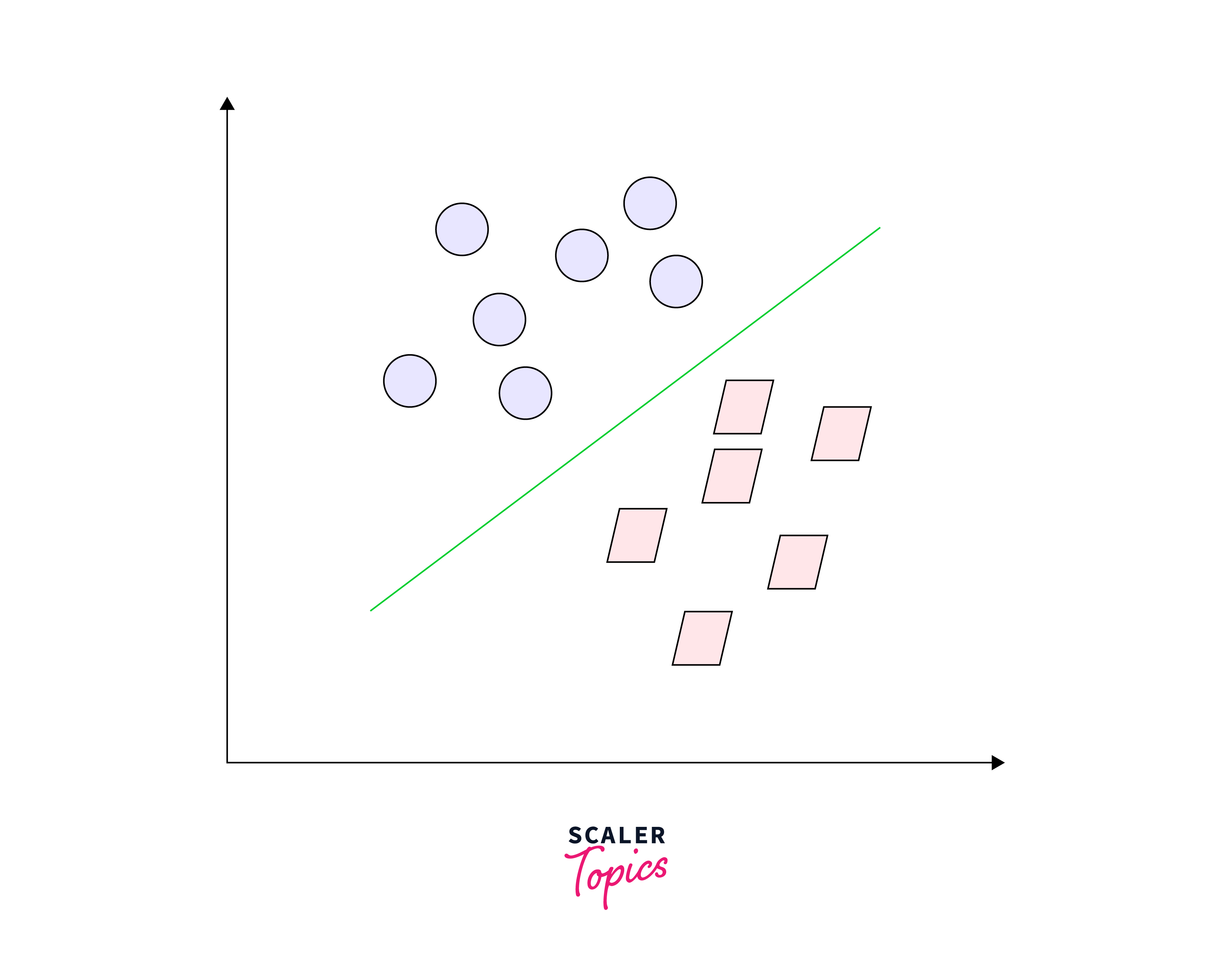
The line effectively divides the classes. This illustrates the fundamental function of SVM – straightforward classification separation. Now, what if the data were arranged in this manner:

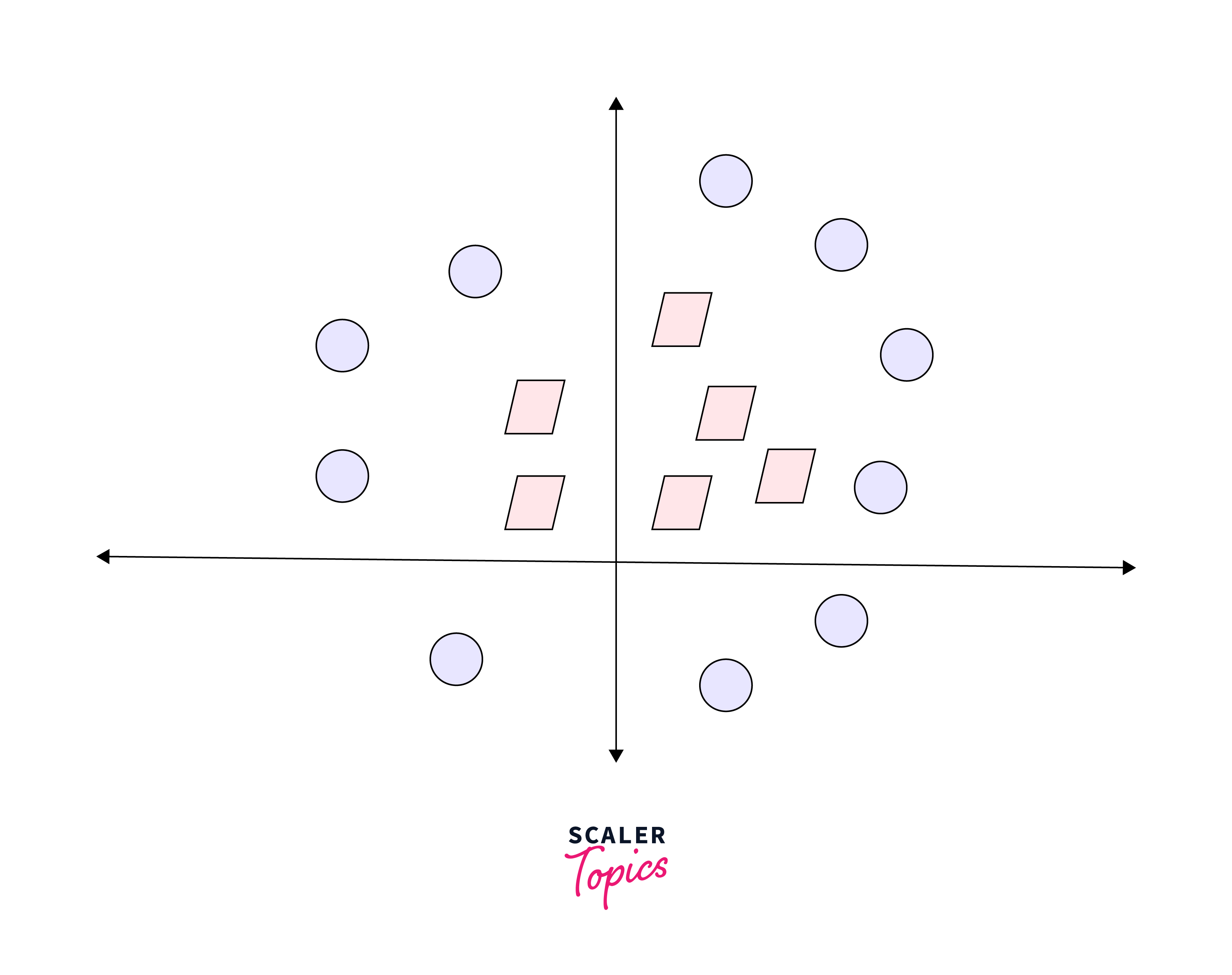
In this scenario, a simple line isn't sufficient to separate these two classes. Therefore, we expand our dimensionality and introduce a new dimension along the z-axis. This enables us to effectively separate the two classes:

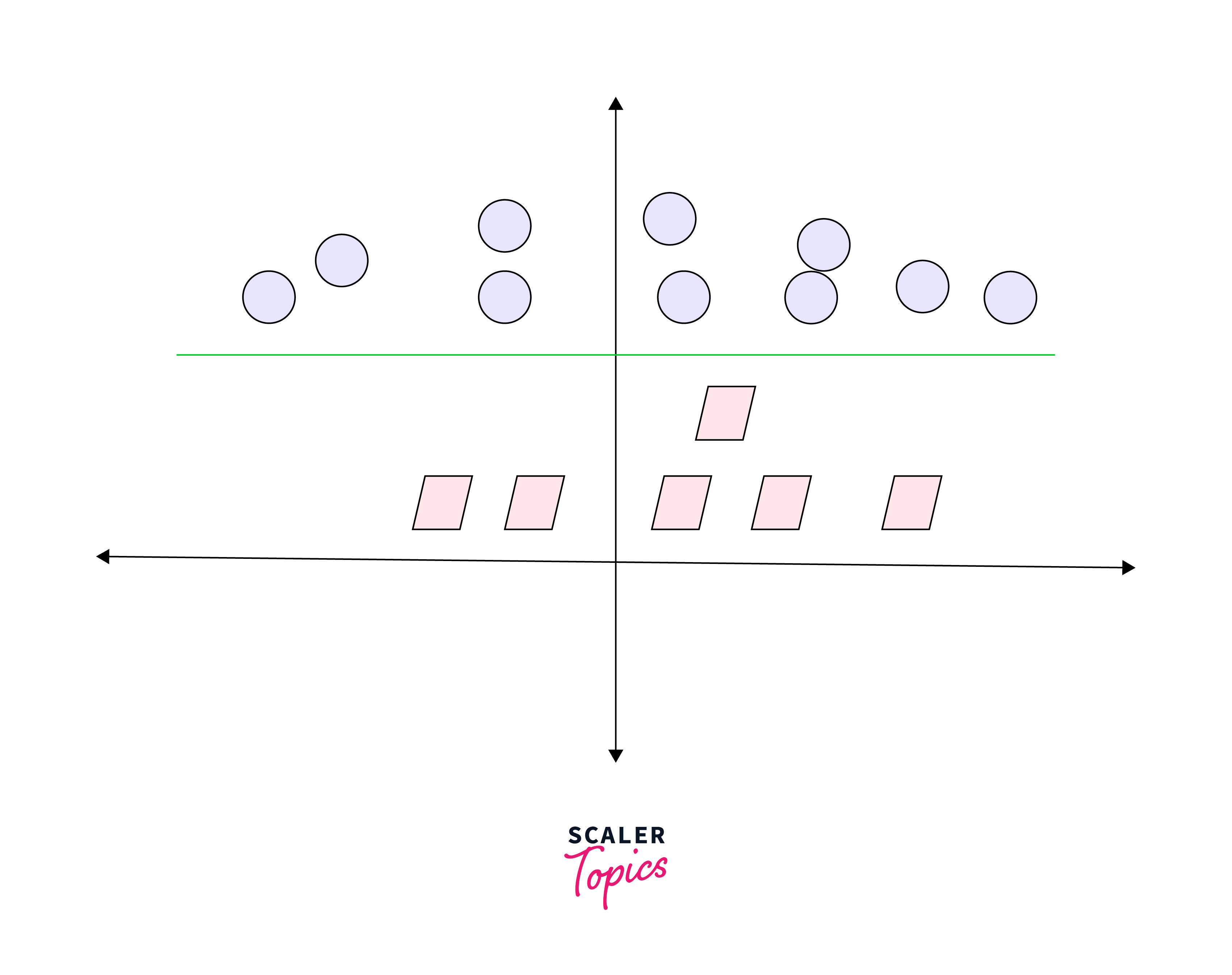
Upon transforming this line back to the original plane, it corresponds to the circular boundary as depicted here:

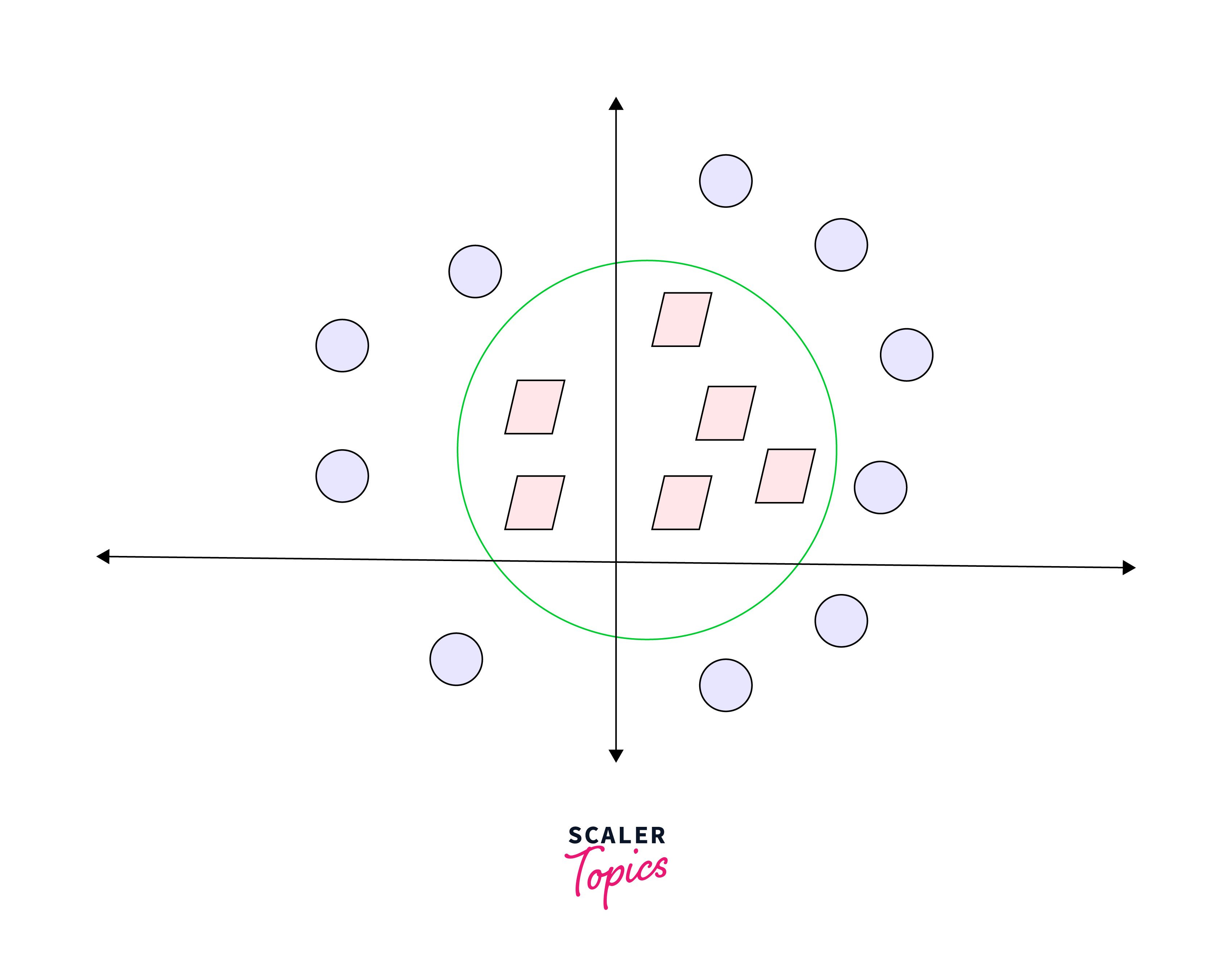
Indeed, that's precisely the essence of SVM! It endeavors to identify a line or hyperplane (within multidimensional space) that effectively segregates the two classes. Subsequently, it classifies a new point based on whether it falls on the positive or negative side of the hyperplane, contingent upon the classes to be predicted.

Hyperparameters of SVM Algorithms

Before delving further, it's crucial to understand several pivotal parameters of SVM:

• Kernel:
  The kernel plays a pivotal role in finding a hyperplane within a higher-dimensional space without inflating computational expenses. Typically, as the dimensionality of data escalates, so does the computational cost. This escalation in dimensionality becomes necessary when we encounter challenges in identifying a separating hyperplane within the given dimension and necessitates transcending to a higher dimension.

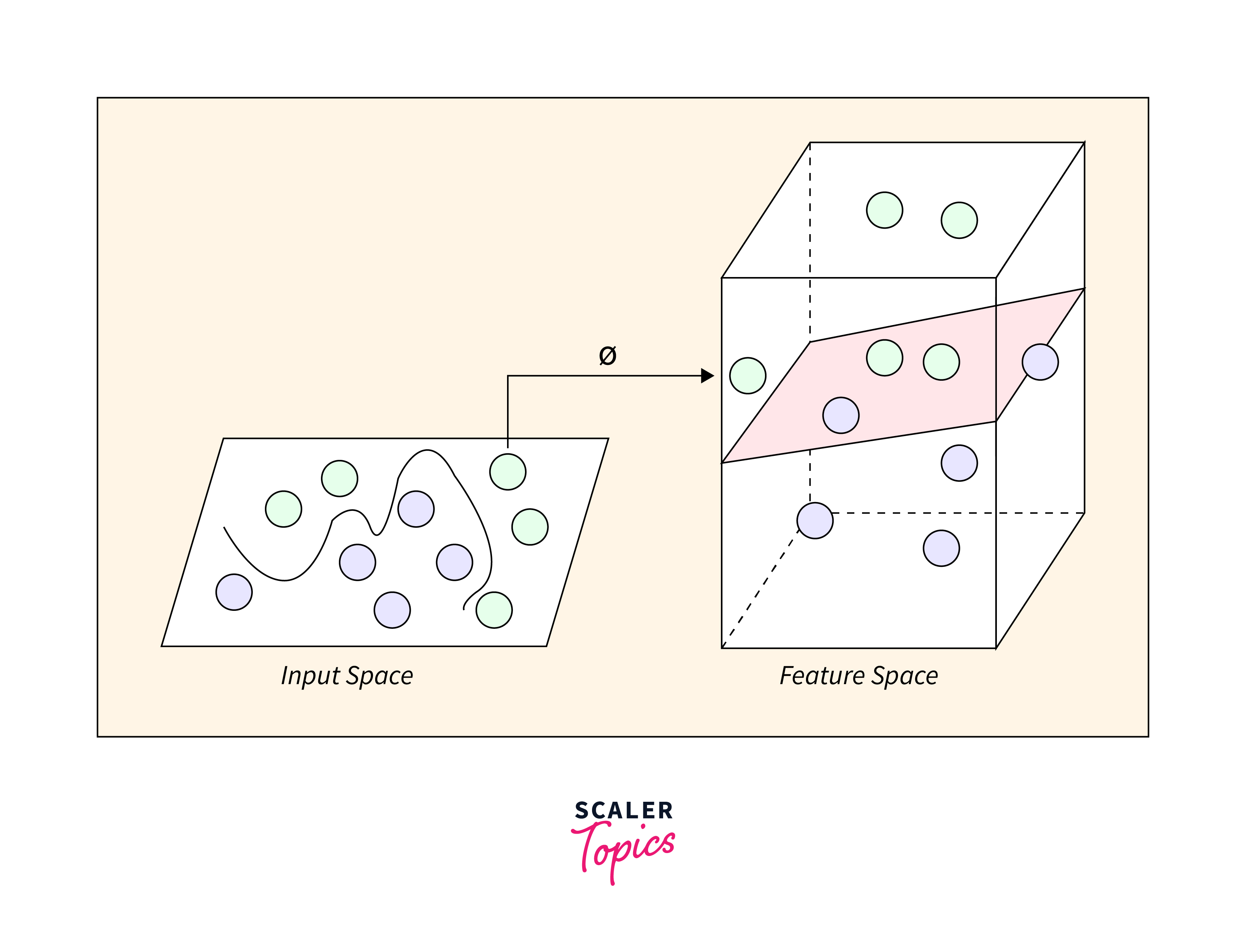
• Hyperplane:
  In SVM, the hyperplane serves as the separating line between two data classes. However, in Support Vector Regression, it transforms into the line utilized for predicting continuous output.

• Decision Boundary:
  Visualize the decision boundary as a delineation line, where on one side reside positive examples and on the other, negative examples. Along this line, examples may be classified as either positive or negative. This principle extends to Support Vector Regression, where similar concepts of SVM are applied.

Kernels

Kernels play a crucial role in Support Vector Machines (SVM) and Support Vector Regression (SVR), as they enable the transformation of input data into higher-dimensional spaces. This transformation facilitates the identification of separating hyperplanes, which are essential for accurate classification and regression.

Types of Kernels

1. Linear Kernel:
   The linear kernel is the simplest type, preserving the original feature space. It computes the dot product between input vectors, making it suitable for linearly separable data. The decision boundary in this case is a straight line or hyperplane.

2. Polynomial Kernel:
   The polynomial kernel introduces non-linearity by computing the dot product raised to a certain power, determined by a user-defined parameter d. This kernel is effective for capturing moderately complex relationships in data, as it can model curved decision boundaries.

3. Radial Basis Function (RBF) Kernel:
   The RBF kernel, also known as the Gaussian kernel, is widely used due to its ability to capture highly non-linear relationships. It transforms data into an infinite-dimensional space, allowing for flexible decision boundaries that can adapt to complex patterns. The RBF kernel is defined by a single parameter $\gamma$, which controls the kernel's smoothness.

Choosing the Right Kernel

Selecting the appropriate kernel for SVM or SVR depends on the nature of the data and the complexity of the relationships between input and output variables. Here are some considerations:

• Linearity:
  If the data is linearly separable, a linear kernel may suffice. However, for non-linear relationships, polynomial or RBF kernels are more suitable.

• Complexity:
  Polynomial kernels with higher degrees can capture more intricate relationships, but they may also be prone to overfitting. RBF kernels offer a balance between flexibility and generalization, making them a popular choice for many applications.

• Computational Cost:
  RBF kernels tend to be more computationally intensive compared to linear or polynomial kernels, especially when dealing with large datasets. Therefore, the choice of kernel should also consider computational resources.

Model Evaluation

Model selection is a critical aspect of building Support Vector Machines (SVM) and Support Vector Regression (SVR) models. It involves choosing the appropriate settings, such as hyperparameters and kernel types, to optimize model performance.

When selecting the best model, it's essential to consider various evaluation metrics that reflect different aspects of model performance. For classification tasks, metrics such as accuracy, precision, recall, F1-score, and ROC-AUC score are commonly used. For regression tasks, metrics such as Mean Absolute Error (MAE), Mean Squared Error (MSE), and R-squared are typically employed.

Support Vector Regression

Support Vector Regression (SVR) is a machine learning algorithm utilized for regression analysis, aiming to find a function that approximates the association between input variables and a continuous target variable with minimal prediction error.

Unlike Support Vector Machines (SVMs) designed for classification, SVR aims to determine a hyperplane that best suits the data points in a continuous space. This involves mapping input variables to a higher-dimensional feature space and identifying the hyperplane that maximizes the margin between itself and the nearest data points while minimizing prediction error.

SVR accommodates non-linear relationships between input variables and the target variable by leveraging kernel functions to map data to higher-dimensional spaces, making it well-suited for regression tasks with complex relationships. SVR operates on the same principle as SVM but is tailored for regression problems.

Implementation of SVR

Implementing SVR involves fitting the model to data and fine-tuning hyperparameters for optimal performance. Let's take a look with some examples:

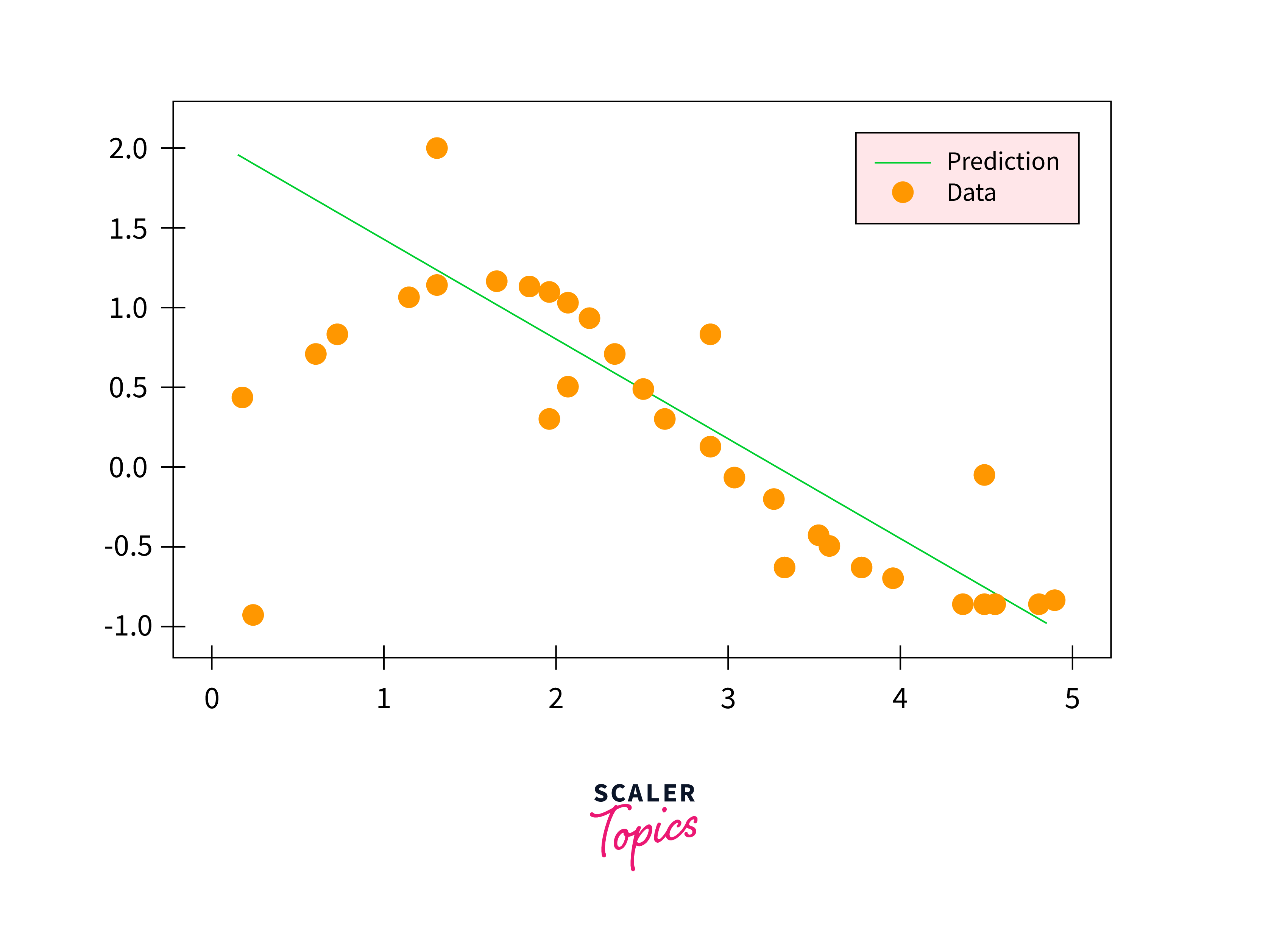
Fitting SVR on Sine Curve Data Using Linear Kernels

Initially, we'll aim to establish baseline results by employing the linear kernel on a dataset exhibiting non-linear characteristics. Subsequently, we'll assess the degree to which the model can accommodate the dataset's complexity.

Output:

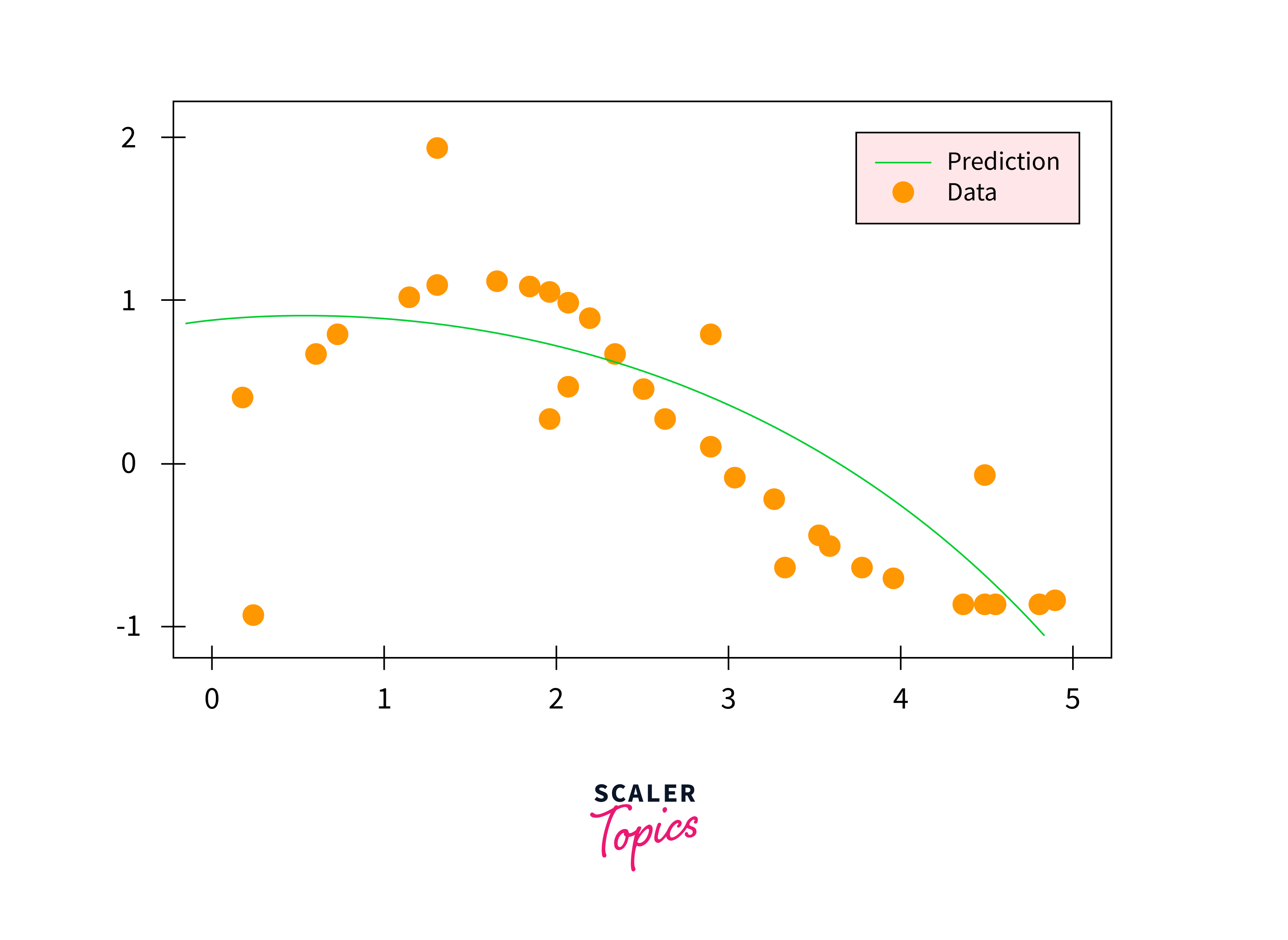
Fitting SVR on Sine Curve Data Using Polynomial Kernels

Next, we'll proceed to train a Support Vector Regression (SVR) model utilizing a polynomial kernel. It is anticipated that this approach will yield slight improvements compared to the SVR model employing a linear kernel.

Output:

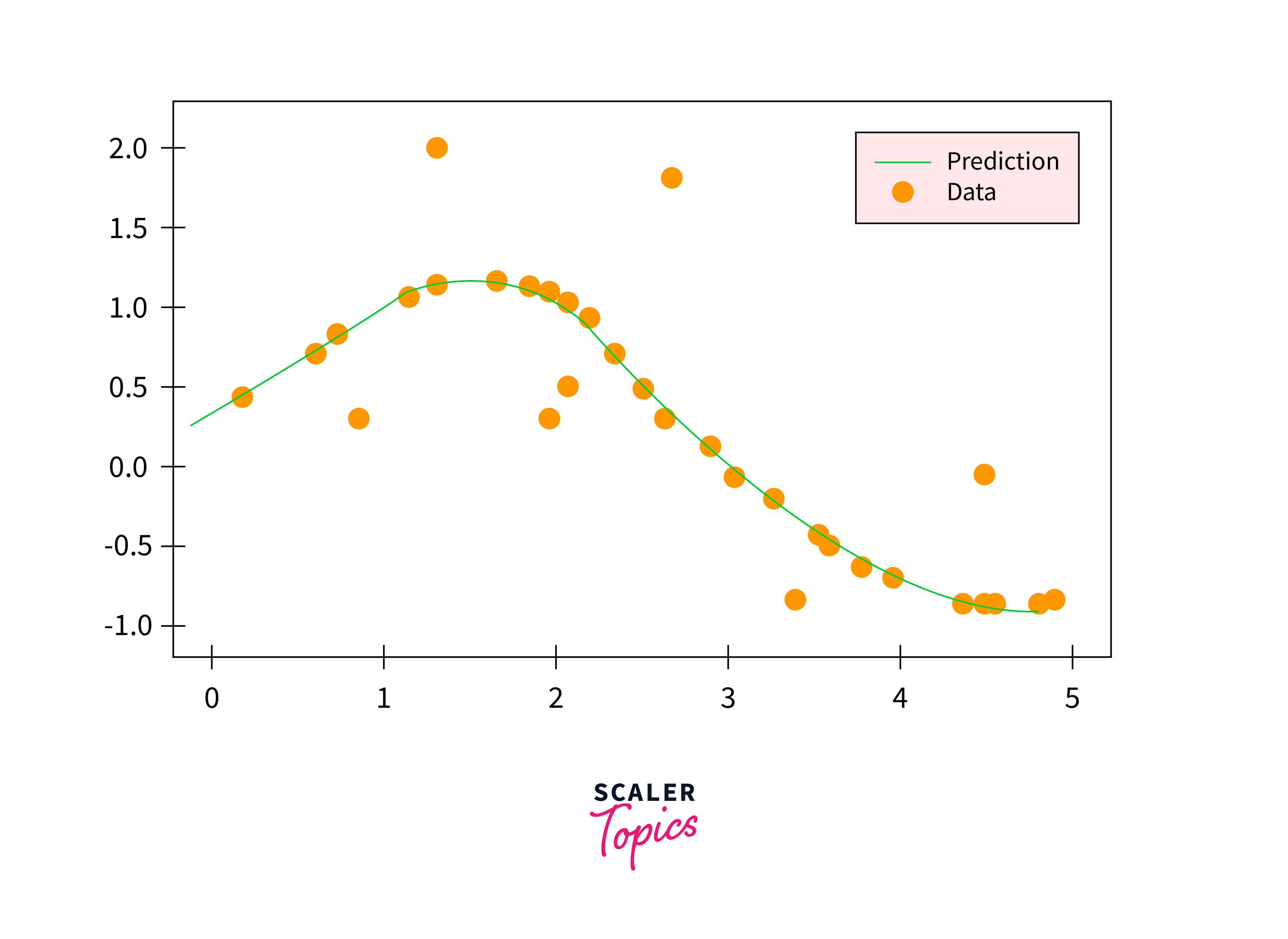
Fitting SVR on Sine Curve Data Using RBF Kernels

Subsequently, we'll employ a Support Vector Regression (SVR) model utilizing an RBF (Radial Basis Function) kernel. This strategy is expected to yield the most optimal results, as the RBF kernel is renowned for effectively introducing non-linearity into our model, potentially enhancing its performance significantly.

Output: