Gaussian Processes with TensorFlow Probability

What are Gaussian Processes (GPs)?

Gaussian Processes (GPs) are a mathematical framework used in machine learning and statistics. They represent a collection of random variables, where any finite subset follows a Gaussian distribution. While GPs can be defined for finite sets, they are often applied to infinite-dimensional spaces, treating them as distributions over functions.

In GPs, you have two essential components: the mean function, which assigns a mean value to each point in the index set, and the covariance function (kernel), which specifies the relationships between different points. The kernel function is crucial as it entirely shapes the properties of functions drawn from the GP. GPs are versatile tools for modelling and uncertainty estimation, commonly used in regression and optimization tasks.

where,

• m is the mean function
• k is the covariance kernel function
• f is the function drawn from the GP
• x[i] are the index points at which the function is observed
• y[i] are the observed values at the index points
• s is the scale of the observation noise.

Introduction to TensorFlow Probability (TFP)

TensorFlow Probability, or TFP, is a specialized library that brings the power of probabilistic thinking and statistical analysis into the TensorFlow framework. By seamlessly combining probabilistic techniques with deep learning, TFP enables us to perform advanced tasks like probabilistic modelling, Bayesian inference, and statistical analysis within the familiar TensorFlow environment.

One of its standout features is the ability to use gradient-based methods for efficient inference through automatic differentiation, making complex probabilistic modelling more accessible and efficient. Additionally, TFP is designed to handle large datasets and models efficiently, thanks to its support for hardware acceleration (such as GPUs) and distributed computing. This makes it a valuable tool for researchers and practitioners working on machine-learning projects that require probabilistic modelling and statistical reasoning.

Fundamentals of Gaussian Processes

To grasp the fundamentals of Gaussian Processes, let's break down the key concepts:

1. Random Variables Collection: A Gaussian Process is essentially an infinite collection of random variables. These random variables are indexed by a set of input points, which can be either finite or infinite. The crucial property of GPs is that any finite subset of these random variables follows a joint Gaussian distribution.

2. Real-Valued Functions: In practical applications, GPs are often used to model real-valued functions. Think of these functions as predictions or estimates that we want to make based on our data.

3. Mean Function (m): The mean function, denoted as 'm,' assigns an expected value to each point in the input space. It represents the central tendency of the functions generated by the GP. However, GPs are quite flexible, and the mean function can be adjusted based on prior knowledge or assumptions about the data.

4. Covariance Kernel Function (k): The covariance kernel function, also known as the kernel, is a critical component of GPs. It defines the relationships between different input points. Specifically, it measures how correlated the function values at two different points are. The choice of kernel function significantly influences the behaviour of the GP model.

5. Function Samples (f): When we sample from a Gaussian Process, we obtain different functions that fit the data. These sampled functions are used for predictions and can vary widely depending on the GP's mean and covariance structure.

6. Observations (x[i], y[i]): In practice, we often have observed data points (x[i], y[i]) where x[i] are the input points, and y[i] are the corresponding output values. GPs allow us to incorporate this observed data to make predictions and quantify uncertainty.

7. Observation Noise (s): GPs can account for observation noise (commonly denoted as 's') which represents the uncertainty or variability in our observed data. This is crucial in real-world scenarios where measurements are not perfectly precise.

Building Gaussian Processes with TFP

Certainly, building Gaussian Processes (GPs) with TensorFlow Probability (TFP) involves several steps. In this implementation, we'll create a GP regression model from scratch using Python and TFP. Ensure you have TFP and TensorFlow installed in your environment.

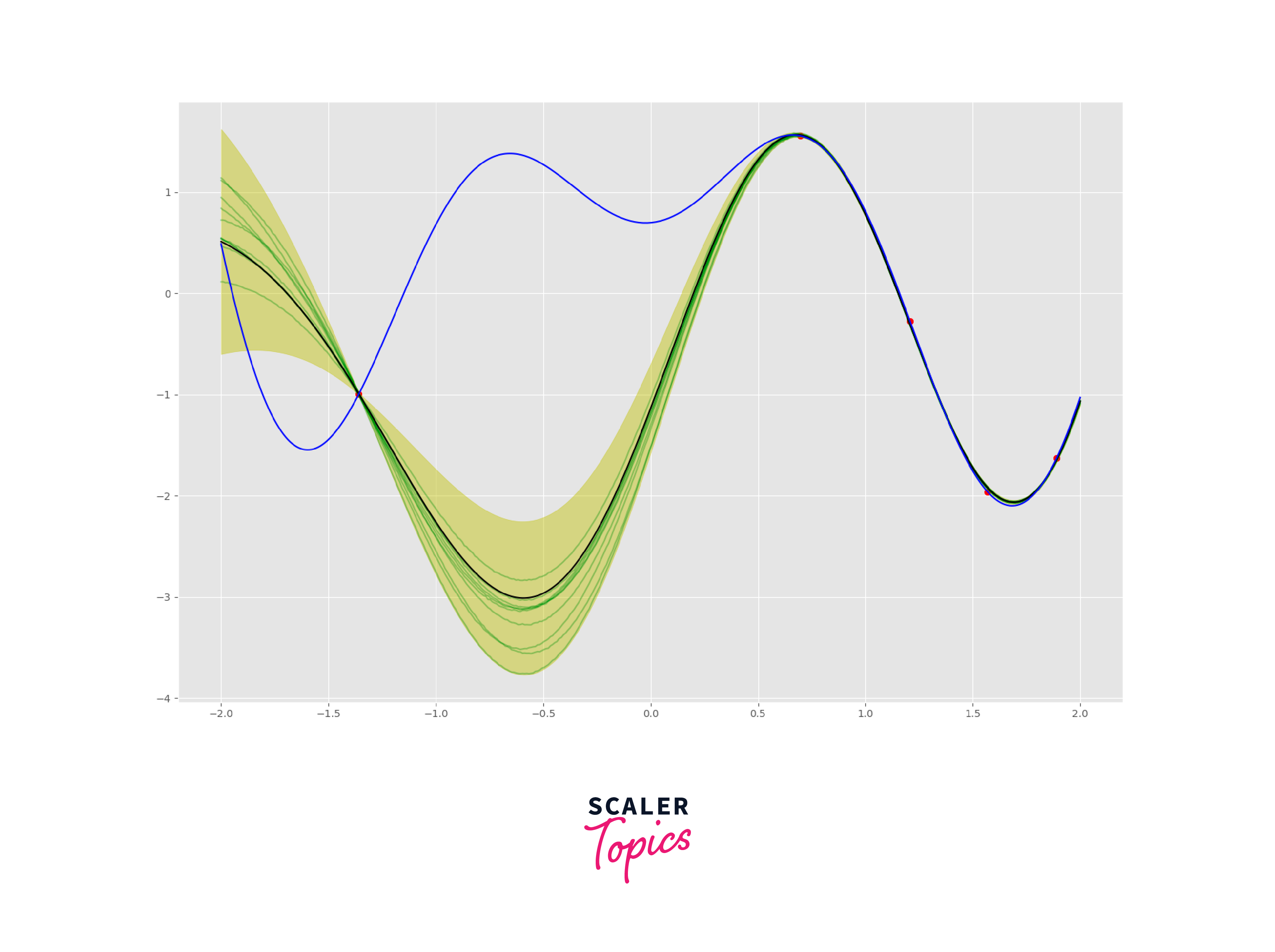
Training Gaussian Processes

Training Gaussian Processes (GPs) involves optimizing the model's hyperparameters to make accurate predictions on training data. Here's a concise overview of the training process:

• Data Preparation: Gather and preprocess your training data, which consists of input features and corresponding target values.
• Kernel Selection: Choose an appropriate covariance kernel function that models the relationships between data points. The kernel's choice impacts the GP's predictive capability.
• Hyperparameter Initialization: Initialize hyperparameters associated with the kernel function, such as length scales and amplitudes. Proper initialization is essential for the optimization process.
• GP Model Definition: Build a GP model using the chosen kernel and training data. This model combines the kernel function, the mean function (often set to zero), and the training dataset.
• Hyperparameter Optimization: Optimize the hyperparameters by maximizing the likelihood of the training data under the GP model. This step can be done using optimization techniques like gradient descent.
• Prediction and Uncertainty Estimation: After optimization, use the trained GP to make predictions for new data points. GPs provide not just point predictions but also uncertainty estimates (variance) for each prediction, essential for assessing the model's confidence.

Uncertainty Estimation with Gaussian Processes

Uncertainty estimation is one of the key advantages of Gaussian Processes (GPs). GPs provide not only point predictions but also a measure of uncertainty associated with those predictions. Here's an explanation of how to estimate uncertainty with GPs:

1. Posterior Distribution: In Gaussian Processes, the predictions for a given input point are represented by a posterior distribution. This posterior distribution combines the prior beliefs about the function (based on the kernel and mean function) with the observed data.

2. Mean Prediction: The mean of the posterior distribution at a specific input point provides the "best guess" or point prediction for the function value at that point. This is often referred to as the "mean function" of the GP.

3. Uncertainty (Variance) Prediction: The variance of the posterior distribution at a specific input point quantifies the uncertainty or the spread of possible function values at that point. It represents how confident the GP is in its prediction. A high variance indicates high uncertainty, while a low variance indicates low uncertainty.

4. Prediction Interval: Using the mean prediction and the uncertainty prediction (variance), you can construct prediction intervals around your point predictions. An A*wide prediction interval suggests high uncertainty, while a narrow interval suggests low uncertainty.

5. Visualizing Uncertainty: Visualizing uncertainty is often done by plotting the mean prediction along with the prediction interval (e.g., $±2$ standard deviations) as shaded regions around the mean. This provides a clear understanding of the range of possible function values.

6. Noise Modeling: GPs can model observation noise. This means that uncertainty estimates take into account the noise in the training data, allowing the model to provide more accurate uncertainty estimates, especially when data measurements have inherent noise.

Gaussian Processes for Time Series Analysis

Tensorflow probability Gaussian process for time series analysis is a powerful approach to model complex temporal patterns and quantify uncertainty. Here's a detailed explanation of how GPs can be applied to time series analysis with TFP:

1. Understanding Time Series Analysis: Time series data consists of observations collected or recorded over successive points in time. Common examples include stock prices, weather data, and sensor readings. Time series analysis aims to uncover patterns, trends, and relationships within this data.

2. Gaussian Processes for Time Series: Gaussian Processes are well-suited for time series analysis because they can model complex, non-linear dependencies in the data. In a time series context, GPs treat time points as the input domain and model the underlying function that generates the data.

3. Kernel Selection: Choosing an appropriate kernel function is crucial. The kernel determines the shape and characteristics of the functions the GP can represent. Common choices for time series data include:

• Squared Exponential Kernel (RBF): Suitable for capturing smooth, continuous variations.
• Periodic Kernel: Useful for modelling cyclical patterns in seasonal data.
• Matérn Kernel: Balances smoothness and non-smoothness in the data.

4. Data Preprocessing: Time series data often require preprocessing steps like differencing, scaling, or removing outliers. Proper data preprocessing enhances the GP's ability to capture underlying patterns.

5. GP Model Construction: Build a GP model using TFP with the chosen kernel function. The GP model should include a mean function (typically set to zero for stationary time series) and the selected kernel.

6. Training and Hyperparameter Tuning: Train the GP model using your time series data. This involves optimizing hyperparameters such as the length scale and amplitude of the kernel. TFP provides optimization tools like gradient descent for this purpose.

7. Prediction and Uncertainty Estimation: After training, use the GP model to make predictions for future time points. GPs provide not only point predictions but also uncertainty estimates (variance) for each prediction. These uncertainties are valuable for quantifying the reliability of forecasts.

Advanced Concepts in Gaussian Processes

Gaussian Processes (GPs) are a rich and flexible framework for probabilistic modelling and regression. Here are some advanced concepts and techniques associated with GPs:

• Sparse Gaussian Processes: Sparse GPs are a crucial concept for efficiently handling large datasets. They use inducing points or a subset of the data to approximate the GP, reducing the computational complexity while preserving accuracy. Techniques like Sparse Variational Gaussian Processes (SVGP) are widely used.
• Multi-Output Gaussian Processes (MOGP): MOGPs extend GPs to handle multiple outputs or tasks simultaneously. They are valuable for modelling scenarios with correlated outputs or when information should be shared between related tasks, making them essential for multi-task learning.
• Deep Gaussian Processes (DGP): Deep GPs stack multiple GP layers to create hierarchical models that capture deep and compositional patterns in the data. DGPs are a bridge between GPs and deep learning, offering probabilistic uncertainty estimates while handling complex, hierarchical relationships.
• Bayesian Optimization with GPs: GPs play a central role in Bayesian optimization, a powerful technique for hyperparameter tuning and optimization tasks. Bayesian optimization uses a GP surrogate model to guide the search for optimal solutions while quantifying uncertainty.
• Transfer Learning with GPs: Transfer learning can be performed using GPs to transfer knowledge from a source task to a target task. This concept is valuable when you have related tasks, allowing you to leverage information from one task to improve performance on another, thus reducing the need for extensive data collection.