Introduction to Probabilistic Modeling with TensorFlow Probability

What is the TensorFlow Probability?

At its core, TensorFlow Probability is an extension of the TensorFlow library that specializes in probabilistic modelling and uncertainty quantification. It offers a diverse set of probabilistic distributions, statistical functions, and inference algorithms. These components collectively empower data scientists to create models that can account for uncertainty, making predictions that come with associated probabilities rather than mere point estimates.

Where is Tensorflow Probability Useful?

TensorFlow Probability finds its utility in a wide array of domains and applications, including:

• Bayesian Inference: TFP is well-suited for Bayesian modelling, allowing for the incorporation of prior knowledge and iterative model refinement. This is particularly useful in situations where data is limited or noisy.

• Healthcare and Medicine: In medical diagnosis and treatment planning, TensorFlow Probability enables the creation of probabilistic models that can capture uncertainties in patient data and assist in informed decision-making.

• Finance and Risk Management: TFP can be leveraged to model financial processes and assess risk. It aids in creating more accurate risk assessments, portfolio management, and credit scoring systems.

• Natural Language Processing: In tasks such as text generation or sentiment analysis, TFP can help quantify the uncertainty in linguistic patterns and provide more nuanced insights.

• Autonomous Systems: TFP is invaluable in autonomous systems like self-driving cars, where uncertainty modelling is crucial for safe decision-making in dynamic environments

• Anomaly Detection: TFP's probabilistic models can effectively identify anomalies in data by recognizing deviations from expected patterns.

Introduction to Uncertainty and its Representation

Uncertainty is an inherent aspect of real-world data and often arises from various sources such as measurement errors, inherent variability, and incomplete information. TensorFlow Probability equips us with versatile tools to represent and manage uncertainty:

• Probabilistic Distributions: TFP offers a wide range of probability distributions (e.g., Gaussian, Poisson, Bernoulli), allowing us to model uncertainty in different types of data.

• Monte Carlo Methods: TensorFlow Probability provides support for Monte Carlo techniques like Markov Chain Monte Carlo (MCMC) and Variational Inference, enabling us to approximate complex probability distributions.

• Bayesian Neural Networks: By integrating Bayesian principles into neural network architectures, TFP enables neural networks to provide not just point estimates but also predictive uncertainty.

• Quantifying and Visualizing Uncertainty: TFP facilitates the quantification and visualization of uncertainty through techniques like confidence intervals and credible intervals.

• Ensemble Methods: TFP supports ensemble modelling, where multiple models are combined to improve predictive performance and uncertainty estimation.

In summary, TensorFlow Probability revolutionizes uncertainty modelling by seamlessly embedding probabilistic reasoning into the TensorFlow ecosystem. With its comprehensive range of tools, TFP empowers practitioners to create more accurate, robust, and reliable models that can handle and leverage uncertainty for better decision-making.

Working Principle of Tensorflow Probability

The working principle of TensorFlow Probability (TFP) revolves around integrating probabilistic modelling and inference techniques into the TensorFlow ecosystem. TFP allows you to express uncertainty and randomness in your machine-learning models, making it possible to handle real-world data with inherent variability.

• TFP seamlessly merges probabilistic and TensorFlow operations, tapping into TensorFlow's graph, autodiff, and optimization prowess.
• Inference algorithms (like MCMC, VI) estimate model parameters based on data, yielding posterior distributions. TFP's integration with TensorFlow ensures efficient computation.
• Graphs visualize model relationships; auto diff computes parameter gradients. This empowers optimization for better model fitting.
• Standard TensorFlow optimizers fine-tune model parameters, combining probabilistic reasoning and optimization.
• TensorFlow Probability excels at uncertainty quantification. Inference generates posterior distributions, offering valuable uncertainty insights for robust predictions and decision-making.

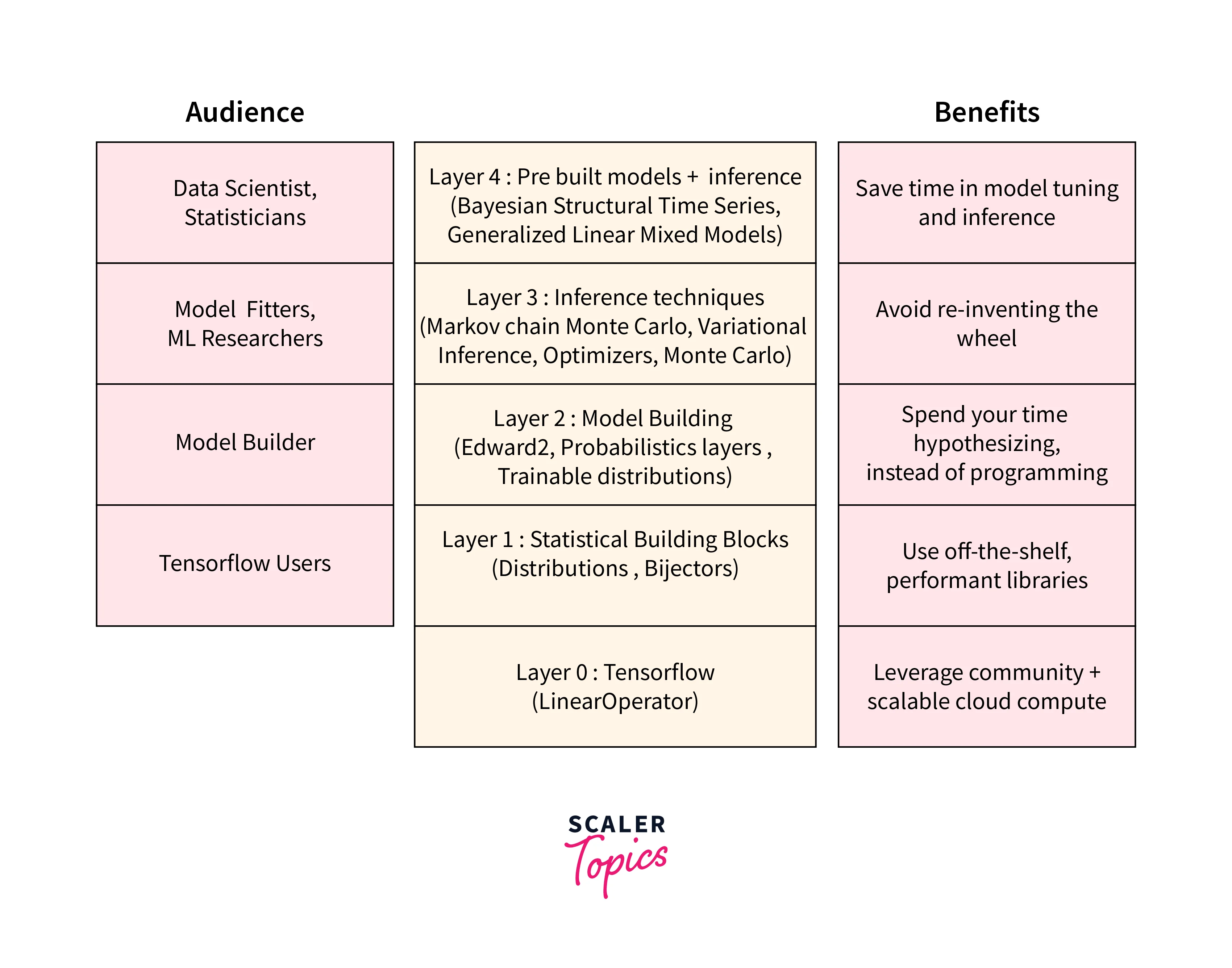
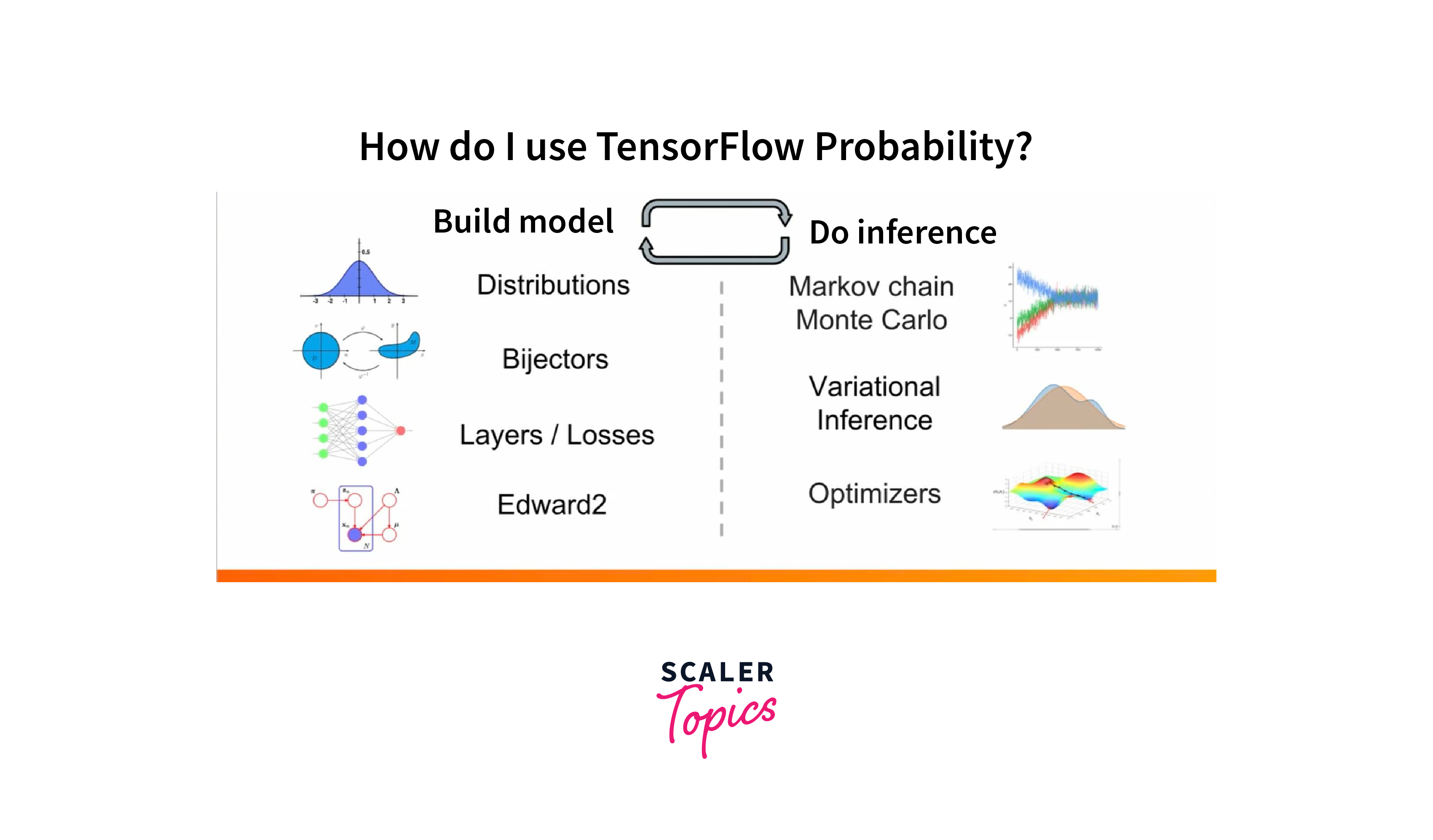
Layer 0: Tensorflow Layer

At its core, TensorFlow Probability is built on top of the TensorFlow framework. It utilizes TensorFlow's powerful computational graph and automatic differentiation capabilities to create and optimize probabilistic models. This layer provides the foundational infrastructure for TFP.

Layer 1: Statistical Building Blocks

This layer includes a collection of probabilistic building blocks, such as probability distributions, bijectors (used for transforming distributions), and random variables. These building blocks serve as the fundamental components for constructing probabilistic models. Probability distributions represent uncertainty and randomness in various quantities, while bijectors enable transformations between different distributions.

Layer 2: Model Building

In this layer, you can construct complex probabilistic models using the statistical building blocks from Layer 1. These models can include Bayesian neural networks, Gaussian processes, hierarchical models, and more. TensorFlow Probability provides a high-level API for defining these models, making it easier to specify the relationships and dependencies between random variables and observations.

Layer 3: Probabilistic Inference

Probabilistic inference is the process of learning from data to estimate the underlying parameters and distributions of a probabilistic model. TensorFlow Probability offers a suite of inference algorithms for performing Bayesian inference, including Markov Chain Monte Carlo (MCMC) methods like Hamiltonian Monte Carlo (HMC) and No-U-Turn Sampler (NUTS), as well as Variational Inference (VI) techniques.

Layer 4: Pre-made Models

TensorFlow Probability provides pre-made probabilistic models and layers that are ready to use. These pre-made models cover a wide range of probabilistic tasks, such as regression, classification, time series analysis, and more. They serve as convenient starting points for building and training complex probabilistic models without having to define everything from scratch.

Setting up TensorFlow Probability

Setting up TensorFlow Probability (TFP) is straightforward and involves a few key steps to get you started with probabilistic modelling and inference.

• Installation: Begin by installing TensorFlow and TensorFlow Probability. You can use pip to install them:

• Importing: Import the required libraries at the beginning of your Python script:

• TensorFlow Compatibility: Ensure you have a compatible version of TensorFlow installed. TFP works with TensorFlow 2.x versions.

• Verification: Verify that your installation was successful by running a quick test:

Now that you have TensorFlow Probability set up, you can start exploring its capabilities, including working with probability distributions.

Distributions in TensorFlow Probability

Distributions are fundamental building blocks in TensorFlow Probability, allowing you to represent uncertainty and randomness in your probabilistic models. TFP provides a wide range of probability distributions that you can use to model different types of data and phenomena.

Creating Distributions:
To create a distribution in TFP, you can simply call the distribution's constructor with the appropriate parameters. For example, to create a Gaussian (Normal) distribution:

In the provided line of code, the loc parameter refers to the mean (average) of the normal distribution, while the scale parameter refers to the standard deviation. The loc parameter sets the centre or average value of the distribution, and the scale parameter controls the spread or dispersion of the distribution's values around the mean.

• Sampling:
  In TensorFlow Probability, sampling from a distribution is achieved through its sample() method.

  For instance, by calling normal_distribution.sample(1000), you generate a sample of size 1000 from the defined normal_distribution, which could be a Gaussian distribution with a specific mean and standard deviation. This sampling process allows you to simulate data points according to the distribution's characteristics, aiding tasks like uncertainty estimation and model validation.

  You can sample from a distribution using its sample() method:

  

• Probability Density Function (PDF):
  Distributions also provide methods to compute the probability density function (PDF) or probability mass function (PMF) at specific points:

• Batched Distributions: You can work with batched distributions to model multiple distributions simultaneously. This is useful when dealing with multiple data points or different groups.

  In the given line of Python code, the loc parameter specifies a list of mean values for each batch, and the scale parameter specifies a list of standard deviations for each batch. This code snippet creates a batch of normal distributions using the TensorFlow Probability library (tfp.distributions.Normal).

• Multivariate Distributions:
  TFP supports multivariate distributions, such as the Multivariate Normal distribution:

  Together, the loc and scale_diag parameters determine the properties of a multivariate normal distribution. The mean vector (loc) positions the distribution in the multivariate space, and the diagonal covariance matrix (scale_diag) governs the dispersion of the distribution's values along each dimension.

Distributions are the foundation for constructing probabilistic models in TensorFlow Probability. You can use them to build complex models by combining distributions and leveraging TensorFlow's computational graph capabilities for inference and optimization.

Bijectors

Bijectors in TensorFlow Probability (TFP) are essential for transforming probability distributions. They allow you to apply reversible transformations to random variables while preserving their underlying probability distribution. Bijectors are crucial for tasks like normalizing flows, which involve transforming a simple distribution (e.g., Gaussian) into a more complex one. TFP provides a wide range of bijector classes, such as Exp, Sigmoid, and Affine.

Layers

In TFP, layers are building blocks for constructing probabilistic models. Similar to traditional deep learning, TFP offers layers for creating various types of probabilistic models, such as Bayesian neural networks.

Create Dataset

Begin by preparing your dataset, ensuring it's appropriately preprocessed and split into training and testing subsets.

Standard Neural Network

A standard neural network, also known as a feedforward neural network, is a foundational architecture in deep learning.

• It comprises layers of interconnected nodes (neurons) that process data in a one-way flow.
• Each neuron applies a weighted sum of inputs, followed by an activation function, to produce an output. Stacked layers enable the network to learn complex patterns from input data.
• These networks excel at tasks like classification and regression. Training involves minimizing a chosen loss function via techniques like backpropagation and gradient descent.
• While effective, standard neural networks lack inherent uncertainty estimation.
• This limitation led to the development of Bayesian Neural Networks, which introduce probabilistic reasoning to enhance predictions and provide uncertainty estimates.

Bayesian Neural Network

A Bayesian Neural Network (BNN) extends traditional neural networks by incorporating probabilistic modelling.

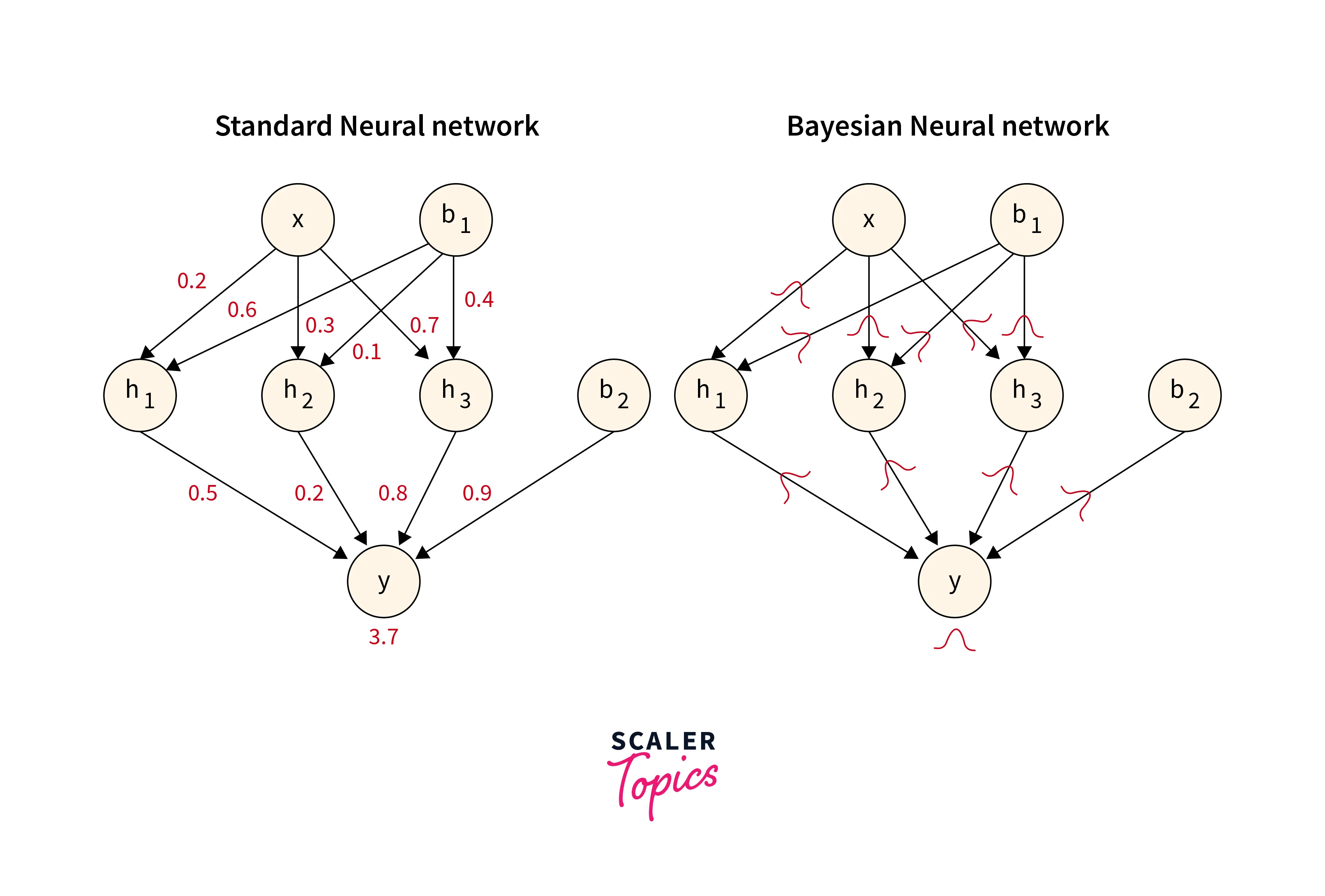
• It captures uncertainty in model parameters, crucial for reliable predictions and decision-making. BNNs assign probability distributions to weights, enabling quantification of prediction uncertainty.
• During training, they optimize the posterior distribution of weights using techniques like variational inference or Markov Chain Monte Carlo. This yields not only point estimates but also uncertainty estimates for predictions.
• BNNs enhance model robustness, especially with limited data, and offer insights into model confidence, aiding more informed choices in various applications, from finance to healthcare.

Model Architecture

For a Bayesian neural network, you'll introduce uncertainty into the model's weights. Replace the dense layers of your standard neural network with probabilistic layers from TensorFlow Probability, like DenseVariational. These layers have a distribution over the weights, allowing for probabilistic reasoning.

Model Configuration

Configure the loss function and optimization strategy. Since you're dealing with a probabilistic model, consider using a suitable probabilistic loss function and optimization approach, such as the ELBO (Evidence Lower Bound) and stochastic gradient descent (SGD).

Train the Model

Train your Bayesian neural network by iteratively updating the model's weights while considering uncertainty in the weight distributions. This involves performing probabilistic inference to estimate the posterior distribution of the weights.

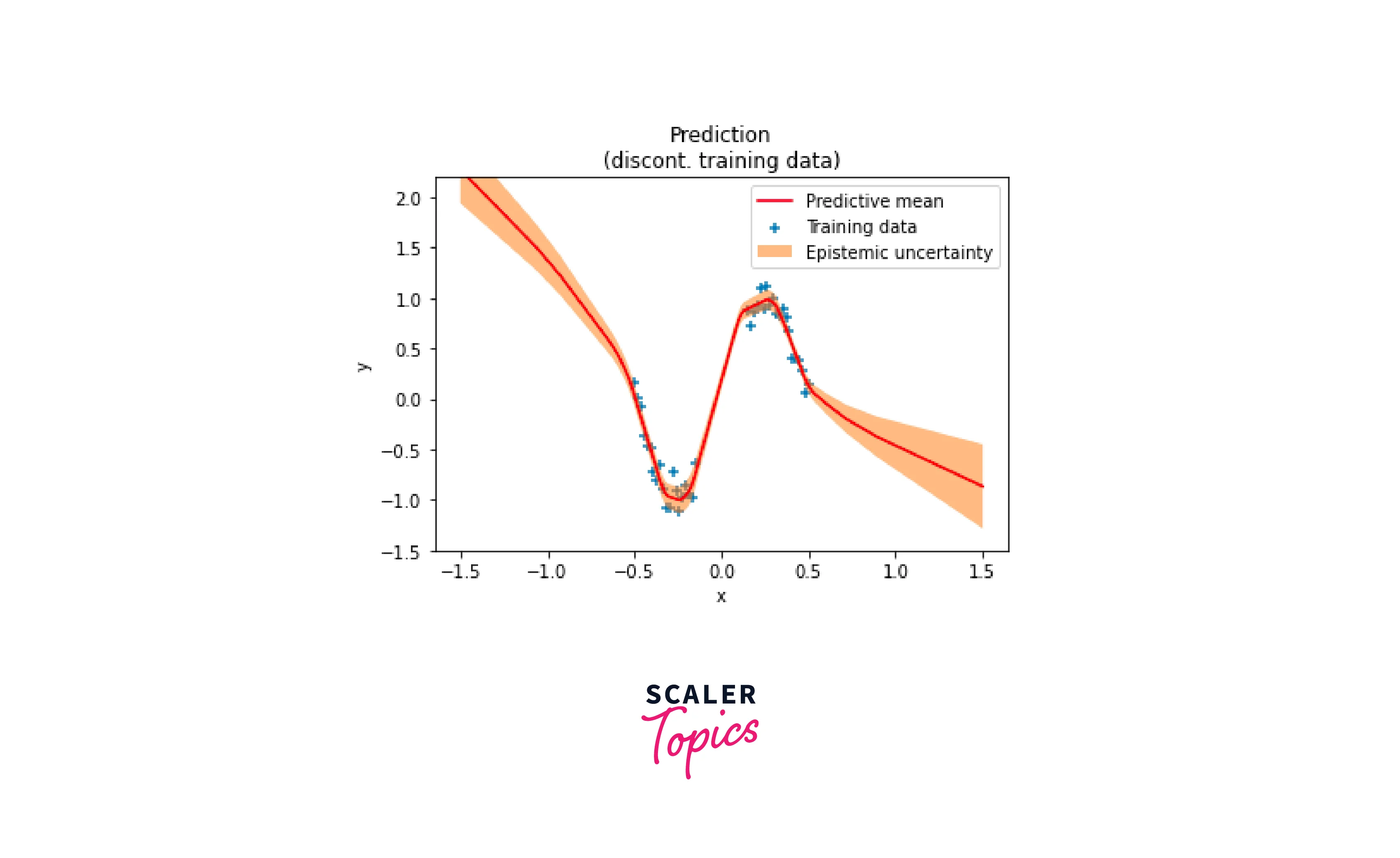
Prediction

To make predictions using your trained Bayesian neural network, you can use the model's predictive distribution. This distribution captures uncertainty in predictions, providing you with not only a point estimate but also a measure of uncertainty.

Build Probabilistic Models with TensorFlow Probability

Building probabilistic models with TensorFlow Probability (TFP) is a systematic process that introduces uncertainty into your machine learning models. Follow these steps to construct and train a simple probabilistic model using TFP:

Step 1: Import Libraries: As the first step, Import TensorFlow and TensorFlow probability.

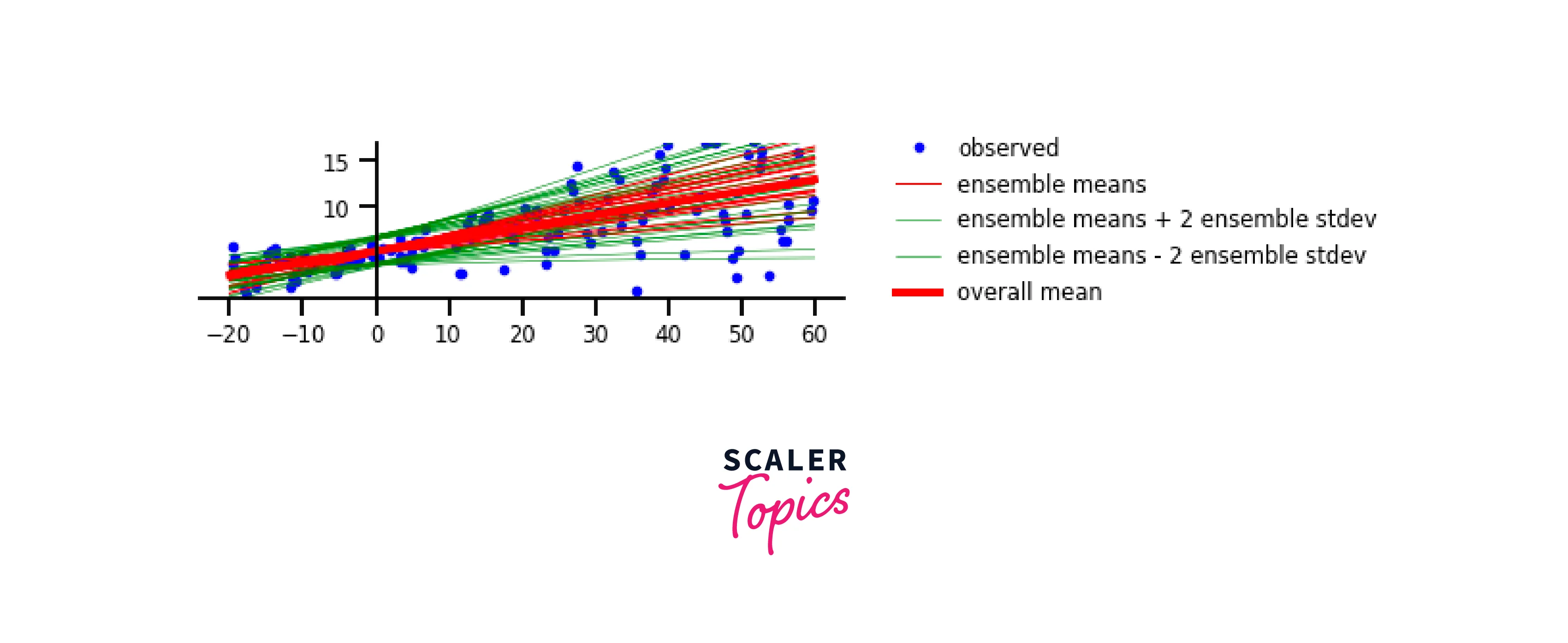
Step 2: Define Data and Variables: Prepare your dataset and define model variables. This code generates synthetic data (X and y) for a linear regression task. It defines two model parameters w and b with probabilistic priors using TensorFlow Probability'sTransformedVariable function.

The w parameter is transformed using the exponential function, introducing positive constraints, while the b parameter remains unconstrained. These probabilistic priors represent the initial beliefs about the parameter values and play a key role in Bayesian modelling for uncertainty estimation.

Step 3: Define Probabilistic Model:
Construct a probabilistic model by specifying the likelihood and prior distributions. In this code segment, a likelihood distribution is defined using TensorFlow Probability (TFP). The likelihood is modelled as a normal distribution, where the mean is determined by the linear combination of X (input data), parameter w, and parameter b, while the standard deviation (scale) is set to 1.0.

Additionally, a prior distribution is established, also as a normal distribution. This prior captures the initial beliefs about the values of the parameters w and b, with a mean of 0.0 and a standard deviation of 1.0.

Step 4: Define Joint Log-Probability Function:

Create a function that computes the joint log probability of the model.

The function joint_log_prob(w, b) calculates the total log-probability of the model by summing the log-likelihood of the observed data (y) under the defined likelihood distribution and the log-probabilities of the prior distributions for parameters w and b. This function is pivotal in Bayesian inference, aiding the estimation of posterior distributions for the parameters.

Step 5: Perform Inference:

Use an inference algorithm (e.g., Hamiltonian Monte Carlo) to estimate the posterior distribution. This code employs Hamiltonian Monte Carlo (HMC) from TensorFlow Probability (TFP) to sample from the posterior distribution of parameters w and b, guided by the joint_log_prob function.

It generates num_samples samples after a num_burnin_steps burn-in period using the defined HMC kernel with specified leapfrog steps and step size. The resulting samples provide insights into the parameter distributions, crucial for understanding uncertainty in Bayesian modelling.

Step 6: Analyze Results:
Analyze the posterior samples to make predictions and infer uncertainty.

Sample Output:

In this sample output, you can see the generated synthetic data, followed by the results of the inference process. The posterior means and standard deviations of the model parameters (w and b) are displayed. Finally, the model uses the estimated parameters to make predictions for new data points. Keep in mind that the actual values might vary due to the random nature of the data generation and the inference process.

Inference and Bayesian Modeling

Inference and Bayesian Modeling are fundamental concepts in TensorFlow Probability (TFP) that enable us to estimate uncertain model parameters and make predictions with quantified uncertainty. Let's explore these concepts in detail with code snippets:

Inference

Inference is the process of learning the likely values of model parameters given observed data. TFP provides various inference algorithms like Markov Chain Monte Carlo (MCMC) and Variational Inference (VI) for this purpose. We'll use VI in this example.

Code Snippet - Variational Inference (VI):

Sample Output:

This output indicates that the estimated value of the parameter w is approximately 1.999872. This value represents our best estimate for the parameter w given the observed data and the specified model.

Bayesian Modeling

Bayesian modeling involves estimating posterior distributions over model parameters, taking into account both prior knowledge and observed data. Bayesian Neural Networks (BNNs) are a common example where we model the distribution of weights in neural networks.

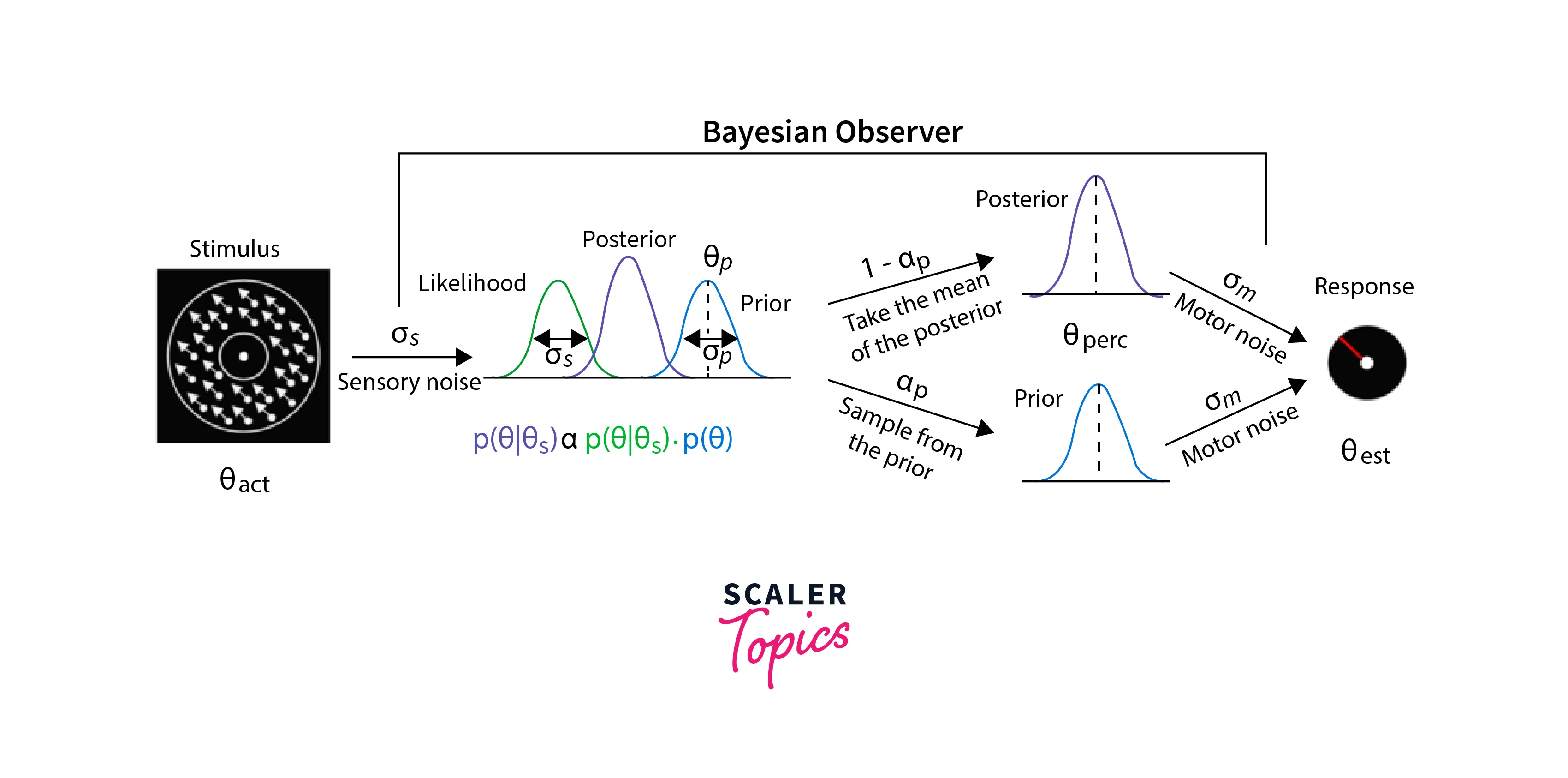
Code Snippet - Bayesian Neural Network (BNN):

Sample Output:

Uncertainty Quantification and Prediction

Uncertainty quantification is a crucial aspect of machine learning, allowing us to measure the uncertainty associated with predictions made by models. TensorFlow Probability (TFP) empowers us to not only make predictions but also provide a measure of how uncertain those predictions are. This is particularly important in decision-making processes where understanding the reliability of predictions is essential.

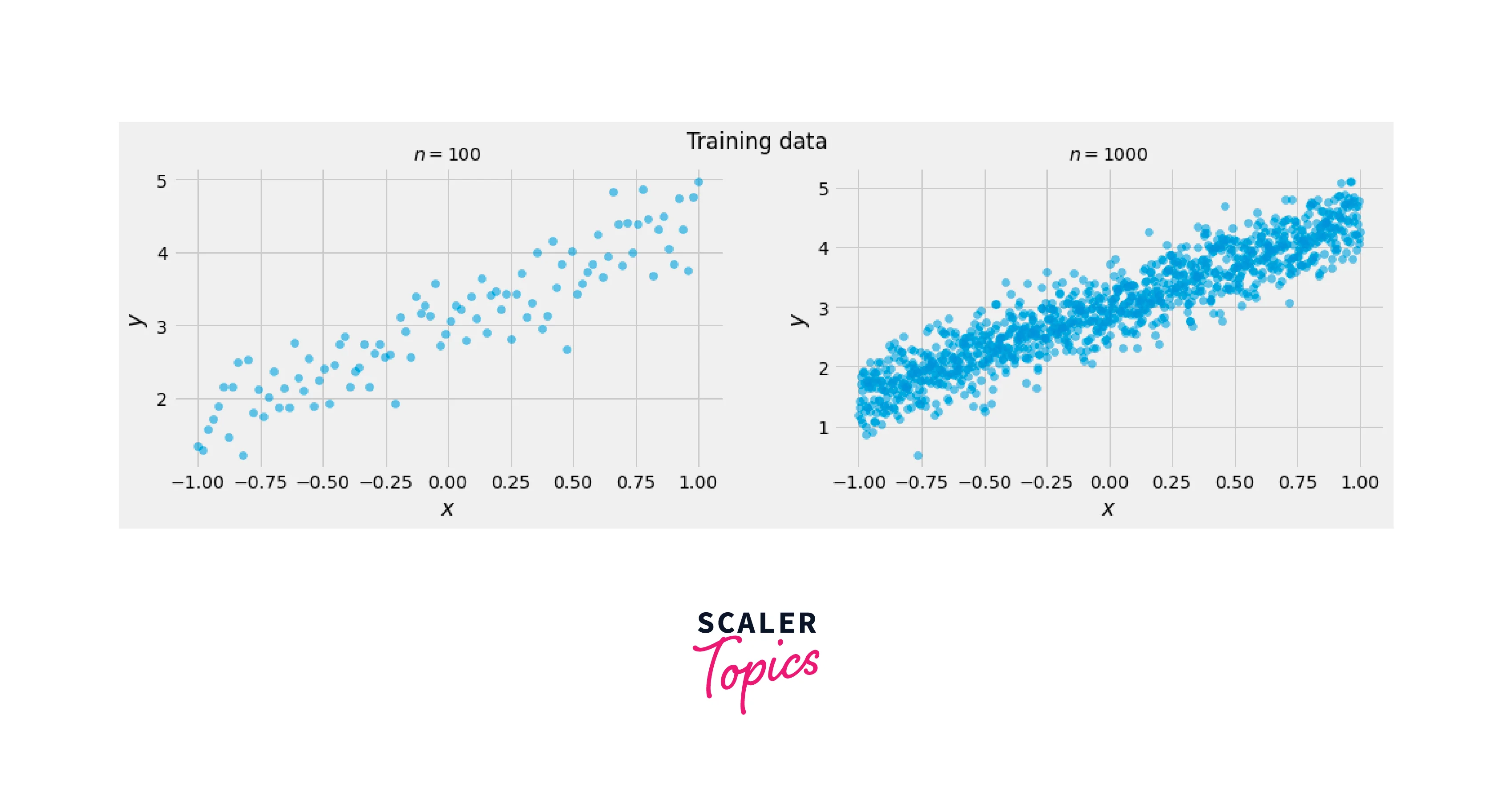
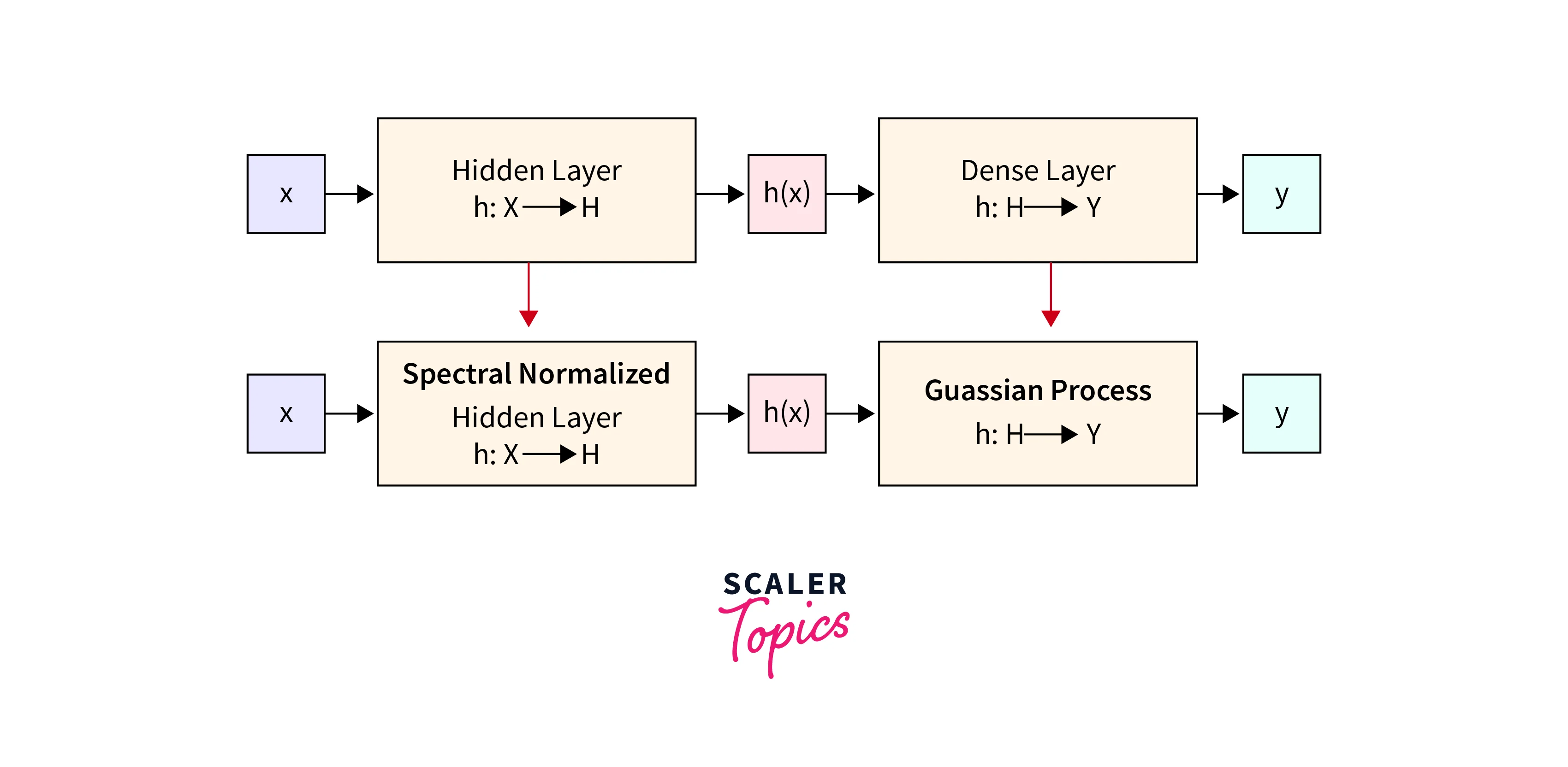
• Bayesian Neural Networks and Uncertainty:
  Bayesian Neural Networks (BNNs), a cornerstone of TFP, naturally facilitate uncertainty quantification. While traditional neural networks offer point estimates, BNNs provide entire distributions over predictions. This distribution encompasses the inherent uncertainty in the model's parameters and the data it has seen.

• Predictive Distributions: Predictive distributions generated by BNNs provide a comprehensive view of uncertainty. Alongside the point prediction, they offer information about the range of plausible outcomes. This enables more informed decisions in various scenarios.

• Uncertainty-Aware Decisions: Uncertainty estimates from predictive distributions guide decision-making. For instance, in a medical diagnosis task, higher uncertainty might prompt seeking additional tests, while lower uncertainty could lead to more confident conclusions.

• Robustness and Outliers: Uncertainty quantification aids model robustness. BNNs can identify data points that deviate significantly from the learned patterns. This is invaluable for anomaly detection or handling noisy datasets.

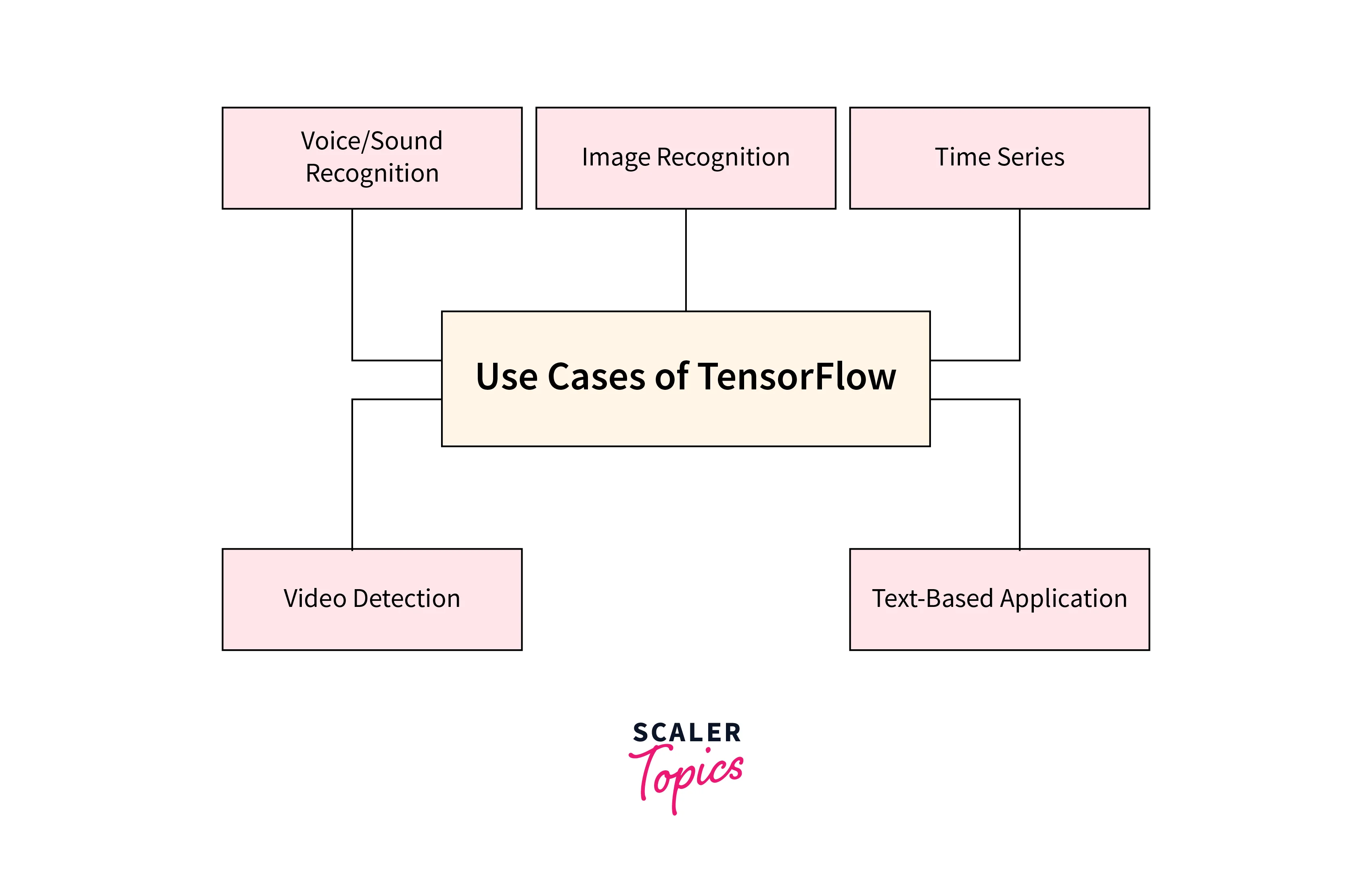
Real-world Applications of TensorFlow Probability

TensorFlow Probability (TFP) extends the capabilities of TensorFlow into probabilistic modelling, opening doors to a multitude of real-world applications that benefit from uncertainty quantification and robust predictions.

• Finance and Risk Management TFP finds a natural fit in finance, where uncertainty assessment is paramount. It models stock prices, estimates market risk, and optimizes investment portfolios while accounting for unpredictable market fluctuations.

• Healthcare and Medical Decision-Making In healthcare, TFP aids medical decision-making by predicting disease progression, assessing treatment outcomes, and providing uncertainty-aware diagnostic insights. It helps doctors make more informed choices for better patient care.

• Autonomous Systems and Safety For autonomous vehicles, TFP's uncertainty quantification is invaluable. It enables safer navigation by identifying potential hazards and assessing their likelihood, guiding the vehicle's responses.

• Industrial Processes and Quality Control In manufacturing, TFP ensures quality control by predicting equipment failures and identifying anomalies. It optimises production processes while accounting for variability in raw materials and operating conditions.

• Environmental Modeling and Climate Studies TFP supports climate modelling, predicting environmental variables and assessing the uncertainty in long-term climate forecasts, aiding policymakers and researchers in understanding potential outcomes.