Bayesian Neural Networks with TensorFlow Probability

What is Bayesian Neural Networks (BNNs)?

Bayesian Neural Networks (BNNs) are a type of neural network that incorporates Bayesian probability theory into their architecture. Unlike traditional neural networks that provide point estimates, BNNs model uncertainty by representing weights and predictions as probability distributions. This allows BNNs to not only make predictions but also express their confidence levels in those predictions. BNNs are particularly useful when dealing with noisy data or limited data availability, as they can account for uncertainty in both the data and the model, making them a valuable tool for robust and reliable machine learning and deep learning applications.

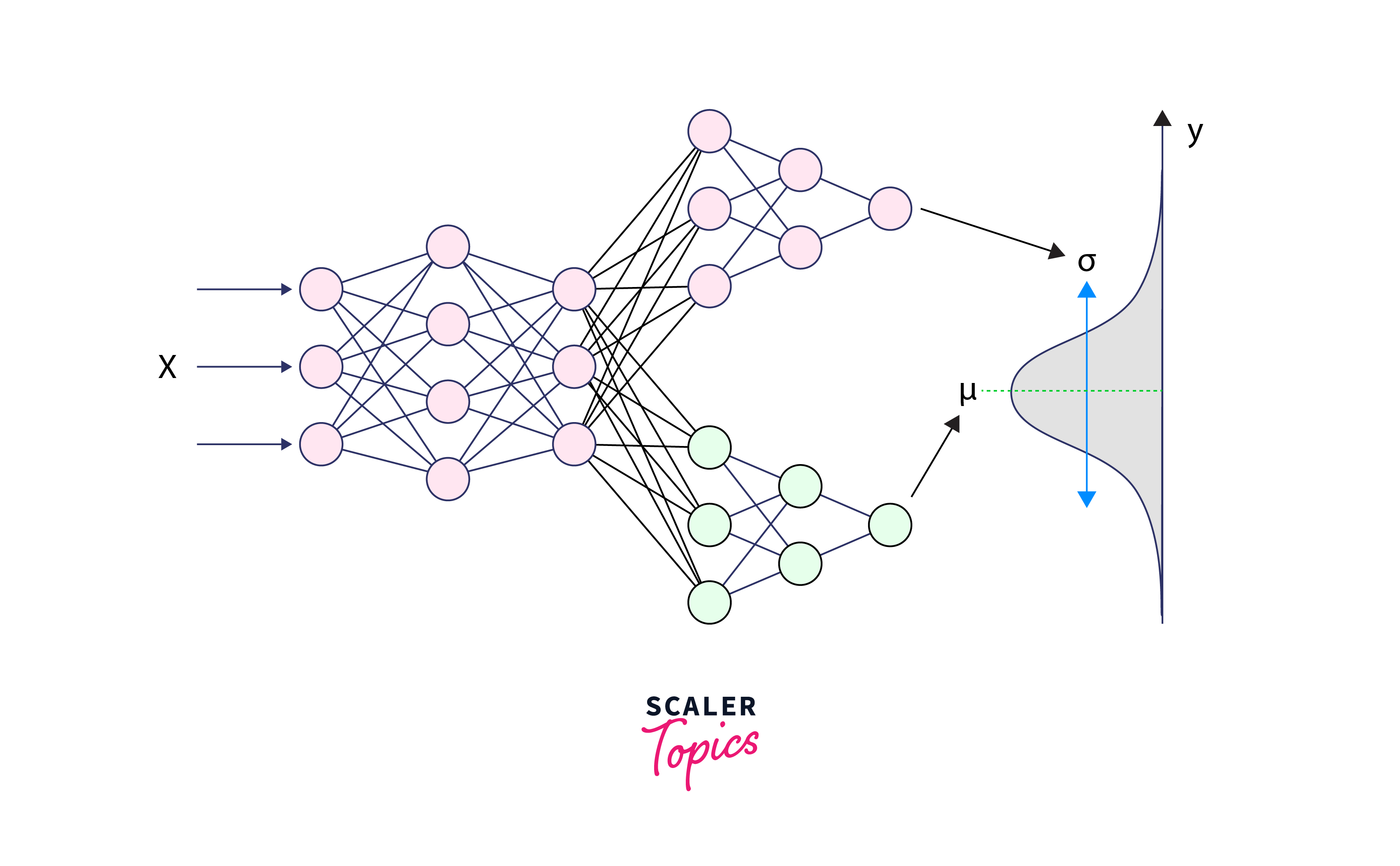
BNNs offer a powerful framework for addressing uncertainties arising from data imperfections and model limitations. We'll delve into the fundamentals of BNNs and provide practical insights on how to construct them.

Introduction to TensorFlow Probability (TFP)

TensorFlow Probability, or TFP, is a specialized library that brings the power of probabilistic thinking and statistical analysis into the TensorFlow framework. By seamlessly combining probabilistic techniques with deep learning, TFP enables us to perform advanced tasks like probabilistic modeling, Bayesian inference, and statistical analysis within the familiar TensorFlow environment.

One of its standout features is the ability to use gradient-based methods for efficient inference through automatic differentiation, making complex probabilistic modeling more accessible and efficient. Additionally, TFP is designed to handle large datasets and models efficiently, thanks to its support for hardware acceleration (such as GPUs) and distributed computing. This makes it a valuable tool for researchers and practitioners working on machine learning projects that require probabilistic modeling and statistical reasoning.

Building Bayesian Neural Networks with TFP

Bayesian Neural Networks (BNNs) offer a powerful approach to tackle uncertainty in deep learning models. By integrating TensorFlow Probability (TFP), we can create BNNs that not only make predictions but also provide probabilistic insights into those predictions. In this section, we'll guide you through the process of constructing tensorflow probability bayesian neural network, enabling you to harness uncertainty for more robust and reliable machine learning applications.

Step 1: Import Necessary Libraries

Step 2: Define the Model Architecture

Here, we use DenseVariational layers from TFP that introduce Bayesian uncertainty into the weights by defining probability distributions over them.

Step 3: Define the Loss Function

Use a negative log-likelihood loss function to account for model uncertainty:

Compile the Model

Training Bayesian Neural Networks

Data Preparation Ensure that your training data (x_train and y_train) are properly formatted.

Model Training

The model will now optimize both the likelihood and the Kullback-Leibler (KL) divergence between the approximate posterior and prior distributions of the weights.

Uncertainty Estimation with Bayesian Neural Networks

Uncertainty estimation is a key benefit of BNNs. You can estimate uncertainty in predictions through Monte Carlo Dropout (MCD) or sampling from the posterior distribution of weights.

1. MCD Estimation:

Monte Carlo Dropout is a simple and effective method for estimating uncertainty in BNNs. It involves repeatedly applying dropout during inference and collecting predictions over multiple runs.

2. Sampling from the Posterior for Uncertainty Estimation:

In a Bayesian Neural Network, you can also directly sample from the posterior distribution of the weights to estimate uncertainty. This method involves drawing multiple weight samples from the posterior distribution and using these samples to make predictions.

3. Predictive Uncertainty Metrics:

Besides mean and standard deviation, you can compute other predictive uncertainty metrics, such as predictive entropy or prediction intervals:

Predictive Entropy:

Measures the uncertainty by calculating the entropy of the predicted probability distribution for classification tasks. Higher entropy indicates higher uncertainty.

Prediction Intervals:

For regression tasks, you can compute prediction intervals (e.g., 95% intervals) to capture the range within which the true value is likely to fall.

Uncertainty estimation with BNNs is a powerful tool for making more informed decisions, understanding model limitations, and ensuring robustness in various applications. The choice between MCD and sampling from the posterior depends on the specific requirements and computational resources available.

Evaluating Bayesian Neural Networks

To evaluate a BNN, you can use standard evaluation metrics like accuracy, precision, recall, and F1-score. Additionally, consider uncertainty metrics such as predictive entropy, calibration plots, and visualizing prediction intervals.

Bayesian Neural Networks for Robustness and Generalization

BNNs naturally provide a measure of model uncertainty, making them valuable for robustness and generalization.

Robustness:

• You can use uncertainty estimates to identify and handle out-of-distribution data or adversarial examples.
• Ensembling multiple BNNs can improve robustness.

Generalization:

• BNNs tend to generalize better because they capture model uncertainty.
• Bayesian dropout can be used for model ensembling to improve generalization.

Remember that building, training, and evaluating BNNs can be computationally expensive due to sampling from posterior distributions. Experiment with the number of samples and other hyperparameters to find a balance between accuracy and computational cost.

Advanced Concepts in Bayesian Neural Networks

Advanced concepts in Bayesian Neural Networks (BNNs) go beyond the basics and provide more sophisticated techniques to improve model performance, robustness, and uncertainty estimation. Here are some advanced concepts:

• Variational Inference:

  Approximates complex posterior distributions in BNNs using tractable families of distributions.

• Hamiltonian Monte Carlo (HMC):

  An advanced MCMC method for faster and less correlated sampling in BNNs.

• Bayesian Model Averaging (BMA):

  Combines predictions from multiple BNNs with different architectures or priors for improved robustness.

• Bayesian Hyperparameter Optimization:

  Uses Bayesian methods to optimize hyperparameters in BNNs efficiently.

• Bayesian Deep Learning Libraries:

  Specialized frameworks like Pyro, Edward, and Probabilistic TensorFlow provide advanced tools for BNNs.

• Heteroscedastic Uncertainty:

  Models varying uncertainty in predictions across different input regions in BNNs.

• Sparse Bayesian Neural Networks:

  Encourages weight sparsity in BNNs for reduced complexity and better generalization.

• Bayesian Transfer Learning:

  Applies knowledge learned from a source task to enhance performance in a related target task using BNNs.

• Bayesian Neural Networks in Reinforcement Learning:

  Utilizes BNNs to capture uncertainty in policy and value functions for efficient exploration and decision-making.

• Scalability Techniques:

  Methods like stochastic gradient Langevin dynamics (SGLD) and No-U-Turn Sampler (NUTS) help scale Bayesian inference in BNNs to handle larger datasets and complex models.