Monte Carlo Methods and Sampling Techniques in TensorFlow Probability

What are Monte Carlo Methods?

Monte Carlo methods, named after the famous casino in Monaco, refer to a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. These methods are particularly valuable for solving complex problems that may be intractable using traditional mathematical techniques.

At their core, Monte Carlo methods use random simulation to estimate mathematical quantities or solve statistical inference problems. By generating a large number of random samples from a probability distribution, these methods can approximate the expectation or probability of a particular event.

Monte Carlo methods find applications in a wide range of fields, including physics, engineering, finance, and computer science. Here are some of the key types of Monte Carlo methods:

• Monte Carlo Integration: This technique is used to numerically approximate complex integrals that are difficult or impossible to solve analytically. By sampling points randomly and applying a suitable weighting function, Monte Carlo integration provides estimates for definite integrals.

• Markov Chain Monte Carlo (MCMC): MCMC methods are essential for Bayesian inference and statistical modeling. They generate a sequence of samples from a probability distribution, often using the Metropolis-Hastings algorithm or Gibbs sampling. MCMC is used to estimate posterior distributions and make probabilistic inferences.

• Monte Carlo Simulation: In this application, Monte Carlo methods are used to model and analyze systems or processes with inherent randomness. For example, in finance, Monte Carlo simulations are employed to evaluate the risk associated with investment portfolios or to price complex financial derivatives.

• Importance Sampling: This technique improves the efficiency of Monte Carlo simulations by giving more weight to samples in regions where the probability distribution is significant. It allows for more accurate estimation with fewer samples.

• Resampling Methods: Techniques like bootstrapping and the jackknife are forms of Monte Carlo resampling. They are used for estimating the sampling distribution of a statistic by repeatedly resampling the data.

In TensorFlow Probability, Monte Carlo methods are extensively utilized to enable probabilistic modeling and Bayesian inference. They allow us to probabilistically model uncertainty, make predictions, and infer unknowns from observed data. In the next section, we will delve deeper into the mechanics and applications of Monte Carlo methods in TensorFlow Probability.

Introduction to TensorFlow Probability (TFP)?

TensorFlow Probability (TFP) is an open-source library developed by Google that provides a wide range of probabilistic modeling and statistical inference tools. It is designed to seamlessly integrate with TensorFlow, the popular machine learning framework.With TFP, developers can easily implement and deploy advanced probabilistic models, enabling them to capture and reason about uncertainties in their data. It provides a comprehensive set of pre-built probability distributions, as well as numerous mathematical operations and algorithms for Bayesian inference.

Monte Carlo methods play a significant role in TFP. By using sampling techniques, TFP allows analysts to estimate expectations, compute marginal probabilities, and perform posterior inference. These methods form the backbone of many algorithms used in TFP, such as Markov chain Monte Carlo (MCMC) and variational inference.

Monte Carlo Sampling Techniques

Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to obtain numerical results. TFP extensively utilizes these techniques to estimate complex expectations, compute marginal probabilities, and perform posterior inference.

One of the primary sampling methods employed in TFP is Markov chain Monte Carlo (MCMC). MCMC constructs a Markov chain that, after a sufficient number of iterations, converges to the desired distribution. This technique allows analysts to generate a set of samples from complex posterior distributions, enabling them to make probabilistic inferences about the data.

Another important sampling technique used in TFP is variational inference. Variational inference approximates complex posterior distributions with simpler, tractable ones. By optimizing a set of variational parameters, TFP constructs an approximate posterior distribution that is computationally efficient to sample from.

Building Probabilistic Models with TFP

TFP provides a comprehensive set of tools and libraries to construct and train probabilistic models. With TFP, you can specify your model as a series of probabilistic distributions, allowing you to capture the uncertainty inherent in real-world data.

To build a probabilistic model with TFP, you start by defining the variables and their respective distributions. TFP supports a wide range of probability distributions, including the usual suspects like Gaussian, Beta, and Gamma distributions, as well as more specialized distributions such as Poisson and Dirichlet. Once you have defined your model, TFP offers a variety of building blocks and functions to perform inference and optimization. You can use MCMC techniques to generate samples from the posterior distribution, enabling you to make probabilistic inferences about your data. Alternatively, you can use variational inference to approximate the posterior distribution and optimize variational parameters for computational efficiency.

we will explore, how to build a probabilistic model for linear regression using TensorFlow Probability (TFP) and walk through each step, from generating synthetic data to training the model and making probabilistic predictions.

• Synthetic Data Generation

Let's start by generating some synthetic data to work with. We'll create a dataset with a linear relationship between the input X and the output Y, adding some Gaussian noise to make it more realistic.

• Data Conversion Next, we convert our data into TensorFlow tensors, which are compatible with TFP and TensorFlow models.

• Defining the Probabilistic Model Now, let's define our probabilistic linear regression model using TFP. This model will not only produce point predictions but also model the uncertainty associated with each prediction.

• Compiling and Training the Model We compile our model using negative log-likelihood as the loss function, which is a common choice for probabilistic models. We also specify the optimizer and learning rate.

• Making Probabilistic Predictions

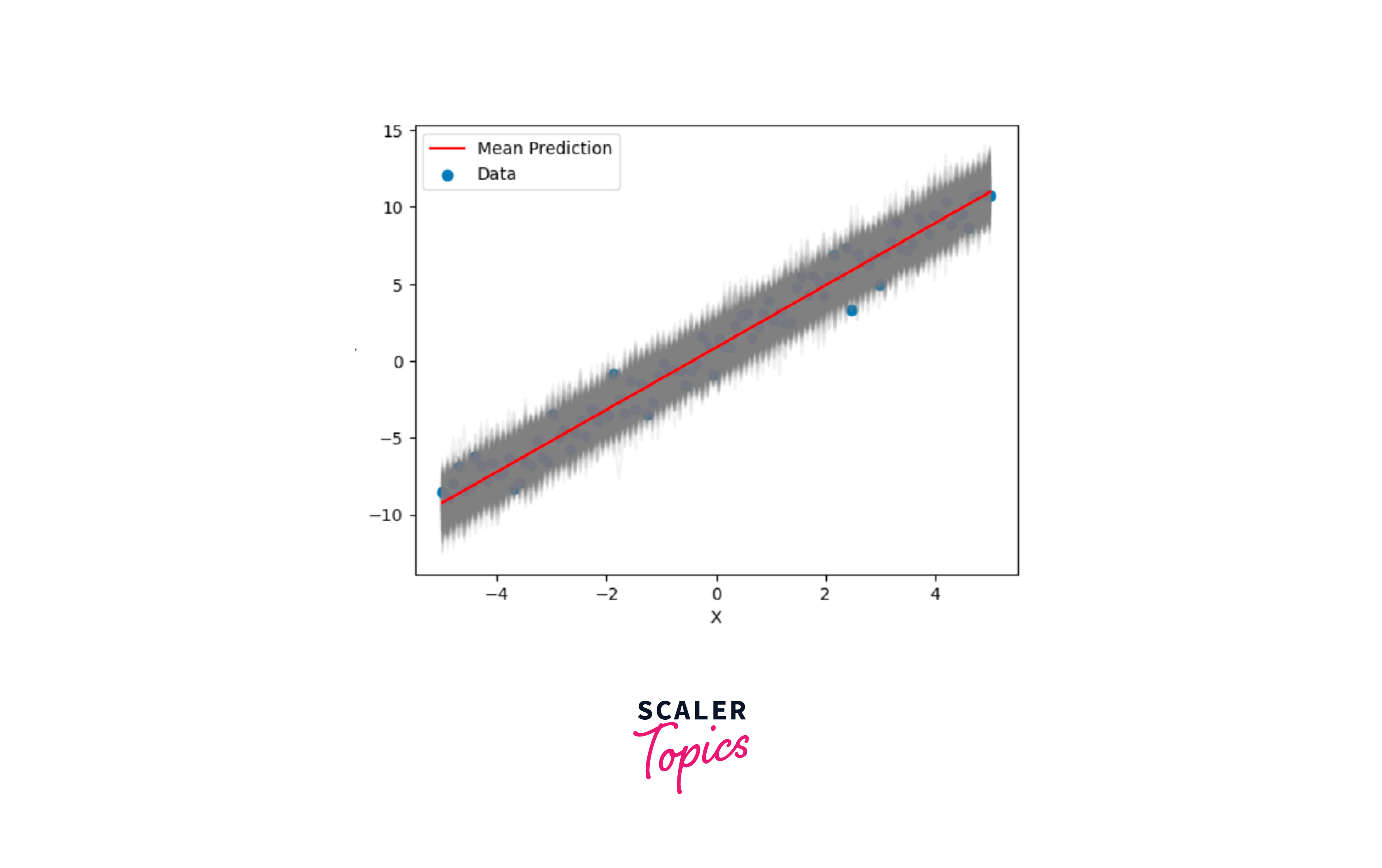
With our trained model, we can now make probabilistic predictions. We sample predictions from the model to account for uncertainty.

• Visualizing the Results Finally, let's visualize our results. We'll plot individual predictions as gray lines and the mean prediction as a red line, giving us a sense of both the model's uncertainty and its overall trend.

Monte Carlo Estimation With TFP

• TFP provides a wide range of functions and tools to perform Monte Carlo estimation. One of the key methods is the Markov Chain Monte Carlo (MCMC), which generates samples from a target distribution by constructing a Markov chain. This technique is particularly useful when dealing with high-dimensional models or when analytical solutions are intractable.

• To perform Monte Carlo estimation with TFP, you can utilize the built-in classes and functions that enable you to define your model, specify priors, and run the MCMC algorithm to generate samples. TFP also offers diagnostic tools to assess the convergence of the Markov chain and ensure the validity of the estimation.

• Using Monte Carlo estimation, you can obtain probabilistic inferences about your model parameters and make predictions based on the generated samples. This approach is especially valuable in Bayesian statistics, as it allows us to quantify uncertainty and make data-driven decisions.

Markov Chain Monte Carlo (MCMC) with TFP

TFP provides an extensive set of tools and classes to implement MCMC in your models. The MCMC algorithm constructs a Markov chain that iteratively generates samples from a target distribution. These samples are then used to approximate the properties of interest, such as the posterior distribution.

To use MCMC in TFP, you will need to define your model and specify the prior distributions. TFP allows you to customize the details of the MCMC algorithm, such as the number of iterations and the proposal distribution. By running the MCMC algorithm, you can generate a set of samples that can be used for inference and prediction.TFP also provides diagnostic tools to assess the convergence and mixing of the Markov chain. These diagnostics help ensure the validity of the estimation and enable you to fine-tune the MCMC algorithm if needed.

Variational Inference with TFP

TFP provides a comprehensive set of tools and classes to implement Variational Inference in your models. The key idea behind Variational Inference is to find the closest approximation to the true posterior distribution by optimizing a set of variational parameters. This optimization problem is typically formulated as minimizing the Kullback-Leibler divergence between the approximating distribution and the true posterior.

To use Variational Inference in TFP, you will need to specify a variational distribution family and define the model and prior distributions. TFP offers a range of variational families, such as mean-field Gaussian or structured Gaussian. The variational parameters are then updated iteratively using gradient-based optimization techniques. By running the Variational Inference algorithm, you can obtain an approximate posterior distribution that can be used for inference and prediction. TFP also provides diagnostic tools to evaluate the quality of the approximation, such as convergence checks and calculating the evidence lower bound.

Bayesian Neural Networks with Monte Carlo Dropout

In this section, we will explore another fascinating application of Monte Carlo methods in TensorFlow Probability (TFP) - Bayesian Neural Networks (BNNs) with Monte Carlo Dropout. BNNs are neural networks that incorporate Bayesian principles to make predictions and estimate uncertainties.

One common challenge in traditional neural networks is that they provide point estimates, which do not account for uncertainty. However, with BNNs, we can obtain a posterior distribution over the network weights, capturing the uncertainty associated with the predictions.we shall see the walkthrough of building a bayesian neural network

To implement BNNs with Monte Carlo Dropout in TFP, we will leverage the dropout technique during both training and inference. Dropout randomly deactivates a subset of neurons during training, which helps the network to generalize better. During inference, we can perform multiple forward passes with dropout, obtaining different predictions. By averaging these predictions, we obtain an estimate of the true posterior distribution.

Now that we have learned how to build and train Bayesian Neural Networks (BNNs) with Monte Carlo Dropout using TensorFlow Probability (TFP), it's time to explore how to evaluate and visualize the uncertainties obtained through Monte Carlo sampling.

One popular way to evaluate uncertainty in BNNs is through the use of predictive variance. Predictive variance measures the variability in predictions by calculating the variance across multiple Monte Carlo samples. A higher predictive variance indicates higher uncertainty in the predictions.

Visualizing the uncertainties can provide valuable insights into the model's behavior. One common method is to plot prediction intervals, which are the ranges of values within which the true value is likely to fall with a certain probability. These intervals can help identify regions of high or low uncertainty in the predictions.

Best Practices and Tips for Monte Carlo Methods with TFP

Monte Carlo methods are widely used in statistics and machine learning for estimating complex probabilistic quantities, and TensorFlow Probability (TFP) is a powerful library for implementing probabilistic models and conducting Bayesian inference. When using Monte Carlo methods with TFP, there are several best practices and tips to keep in mind:

• Understand the Problem: Before diving into TFP and Monte Carlo methods, make sure you have a clear understanding of the problem you're trying to solve and the probabilistic model you're working with. Monte Carlo methods are especially useful for complex probabilistic models.

• Use TFP Distributions: TFP provides a wide range of probability distributions that are essential for Monte Carlo simulations. Utilize these distributions to represent your model's random variables and their dependencies.

• Select an Appropriate Sampling Method:

  • MCMC (Markov Chain Monte Carlo): Consider using MCMC algorithms like Hamiltonian Monte Carlo (HMC) or No-U-Turn Sampler (NUTS) for Bayesian inference. TFP provides these methods via the tfp.mcmc module.

  • Variational Inference: TFP also supports variational inference methods that can be useful for approximating complex posterior distributions.

• Tune Hyperparameters: When using MCMC algorithms, tune hyperparameters such as the step size, number of leapfrog steps, and the number of samples to ensure good convergence and efficient sampling. TFP provides tools to help with this, such as the tfp.mcmc.sample_chain function.

• Use Vectorization: Whenever possible, vectorize your operations to take advantage of TensorFlow's computational efficiency. TFP is built on TensorFlow, and vectorized operations can significantly speed up your simulations.

• Monitor Convergence: When using MCMC, it's crucial to monitor the convergence of your chains. Plot and analyze diagnostic metrics like trace plots, autocorrelation plots, and the Gelman-Rubin statistic (R-hat) to ensure that your chains have converged to the target distribution.

• Use Parallelization: TFP and TensorFlow can benefit from parallelization, especially when dealing with multiple chains or independent simulations. Utilize TensorFlow's parallelism capabilities to speed up computations.

• Prior Knowledge: Incorporate prior knowledge into your models. TFP allows you to specify prior distributions for your parameters, which can improve the efficiency of Bayesian inference.

• Use Jupyter Notebooks: Consider using Jupyter notebooks for interactive exploration and visualization of your Monte Carlo simulations. This can be especially helpful for gaining insights into your models and debugging.

• Performance Optimization: If you're working with large datasets or complex models, consider optimizing the performance of your code. Techniques like batching and caching can be beneficial.