Simple Regression using TensorFlow

Understanding Linear Regression

Linear regression is a fundamental and widely used statistical technique for modeling the relationship between a dependent variable and one or more independent variables. It serves as the building block for various advanced regression models and machine learning algorithms.

At its core, linear regression aims to find the best-fitting line or hyperplane that represents the relationship between the input variables (independent variables) and the output variable (dependent variable). It assumes a linear relationship, meaning the output variable can be expressed as a linear combination of the input variables.

Let's start with the simplest form of linear regression, known as simple linear regression. In this case, we have one independent variable and one dependent variable. The relationship can be expressed as:

$y = (m * x) + c$

Here,

• y is the dependent variable
• x is the independent variable
• c is the y-intercept
• m is the slope of the line.

The goal of linear regression is to estimate the values of c and m that the distance between the actual points and the points on the line are minimum(line of best fit) for the given data.

Linear regression, a widely used statistical technique, has certain assumptions and limitations that are important to consider when applying it in practice, including within TensorFlow regression. Let's discuss these assumptions and limitations:

Assumptions of Linear Regression:

1. Linearity:

   Linear regression assumes a linear relationship between the dependent variable and the independent variables. This means that the model assumes the relationship can be accurately represented by a straight line.

2. Independence:

   Linear regression assumes that the observations are independent of each other. The presence of autocorrelation or dependencies among the observations violates this assumption.

3. Homoscedasticity:

   Homoscedasticity assumes that the variance of the errors is constant across all levels of the independent variables. In other words, the spread of the residuals is consistent.

4. Normality:

   Linear regression assumes that the residuals follow a normal distribution. This assumption is important for hypothesis testing and confidence interval calculations.

5. No Multicollinearity:

   Linear regression assumes that the independent variables are not highly correlated with each other. Multicollinearity can make it challenging to determine the individual impact of each variable on the dependent variable.

Limitations of Linear Regression

1. Linear Assumption:

   Linear regression is limited to capturing linear relationships between variables. It may not be suitable for datasets with nonlinear relationships, as the model may fail to capture the complexity of the data.

2. Outliers:

   Linear regression is sensitive to outliers, which are extreme values that can heavily influence the model's results. Outliers can distort the estimated coefficients and affect the overall model performance.

3. Overfitting:

   Linear regression can be prone to overfitting when the model becomes too complex for the available data. This can happen when there are too many variables or polynomial terms included in the model relative to the number of observations.

4. Limited Handling of Categorical Variables:

   Linear regression inherently assumes numeric input variables. While techniques like one-hot encoding can be used to include categorical variables, linear regression may not fully capture the complexities and interactions of categorical predictors.

5. Non-robustness to Violations:

   Linear regression assumptions, such as linearity and normality of residuals, need to be carefully considered. If these assumptions are violated, the model's estimates and predictions may become unreliable.

When applying linear regression within TensorFlow regression, it is essential to be mindful of these assumptions and limitations.

Data Preparation

Data preparation is a critical step in building accurate and reliable tensorflow regression models. It involves organizing, cleaning, and transforming the raw data into a format suitable for training and evaluating a linear regression model. Data preparation involves several steps including:

1. Data Cleaning and Exploration:

   This involves identifying missing values, outliers, and inconsistencies. Cleaning the data by handling missing values, correcting errors, and addressing outliers is essential to ensure the integrity of the tensorflow regression model.

2. Feature Selection:

   Feature selection plays a vital role in linear regression. It involves identifying the relevant independent variables that contribute meaningfully to the prediction of the dependent variable.

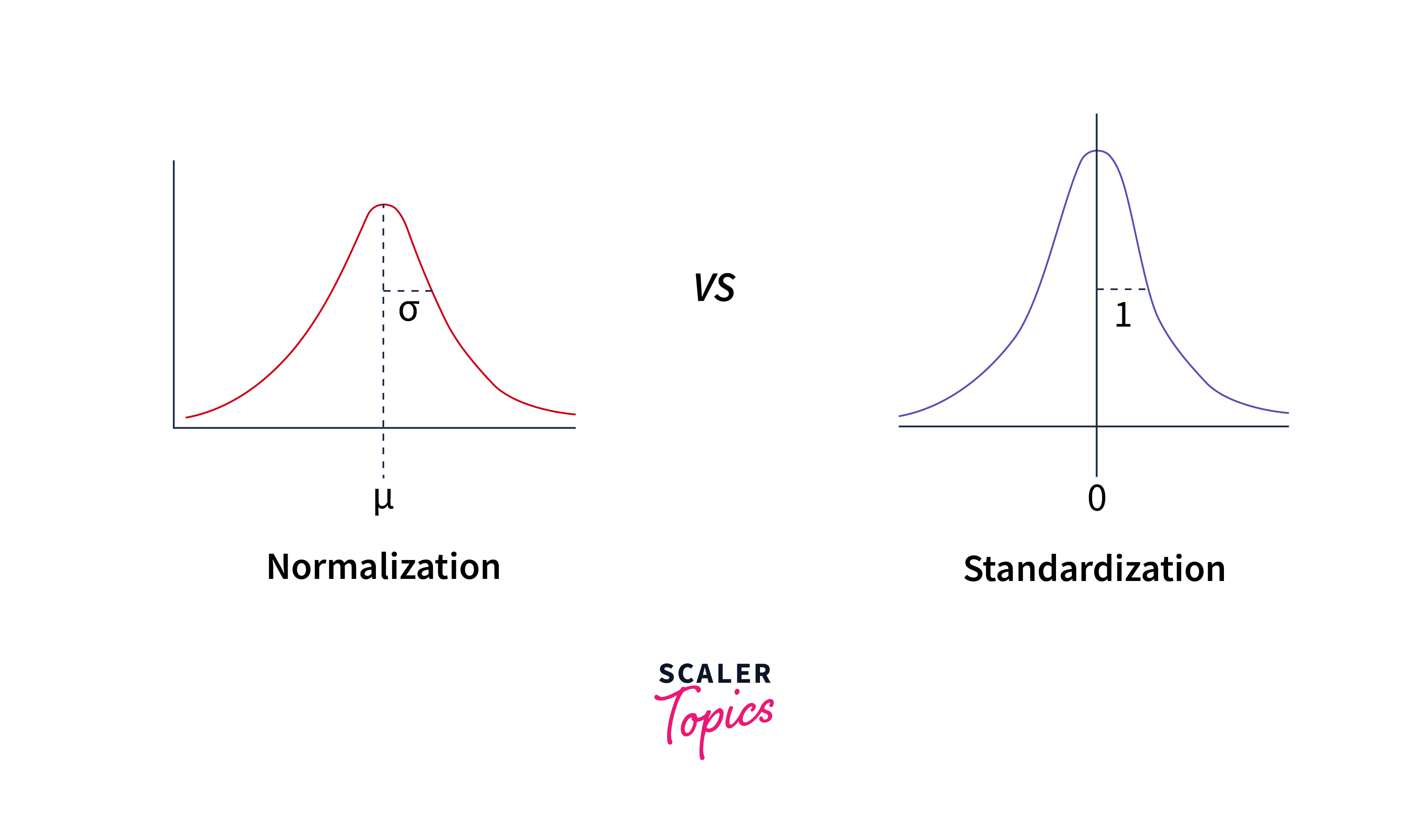
3. Feature Scaling and Normalization:

   In linear regression, it is important to ensure that the independent variables are on a similar scale to avoid biasing the model towards features with larger values. Feature scaling techniques, such as standardization (mean centering and scaling by standard deviation) or normalization (scaling to a range of 0 to 1), can be applied to bring the features to a comparable scale.

Finally, the data needs to be appropriately formatted for TensorFlow regression model. This typically involves converting the data into tensors, which are multidimensional arrays that TensorFlow can efficiently process.

The features and the target variable must be converted to TensorFlow's tf.Tensor objects. This conversion ensures compatibility with TensorFlow's computational graph and enables seamless integration with TensorFlow's regression models.

By following these data preparation steps using TensorFlow, you can ensure that your data is clean, well-structured, and ready to be used for training and evaluating linear regression models.

Building a Simple Linear Regression Model

Now let's start building a linear regression model using TensorFlow.

Step 1: Imports

To begin, we import the required libraries for our linear regression model using TensorFlow. We include TensorFlow itself, along with other standard libraries such as NumPy and Matplotlib for data manipulation and visualization.

Step 2: Setting up TensorFlow

We set up the TensorFlow environment for the tensorflow regression model by defining the necessary placeholders for input data and model variables.

• The code utilizes the compat.v1 module to ensure compatibility with TensorFlow 1.x. This allows you to run code that was originally written for TensorFlow 1.x in newer versions of TensorFlow.

• Placeholders are used to hold the input data during the model's training or inference phase. In this code, X and Y are created as placeholders for the input features and target values, respectively. The data type for both placeholders is set to "float".

• Variables are TensorFlow objects that hold and update the model's parameters during training. In this code, W and b are defined as variables to represent the weight and bias of the tensorflow regression model. They are initialized with random values using 'np.random.randn()'.

Step 3: Data Collection

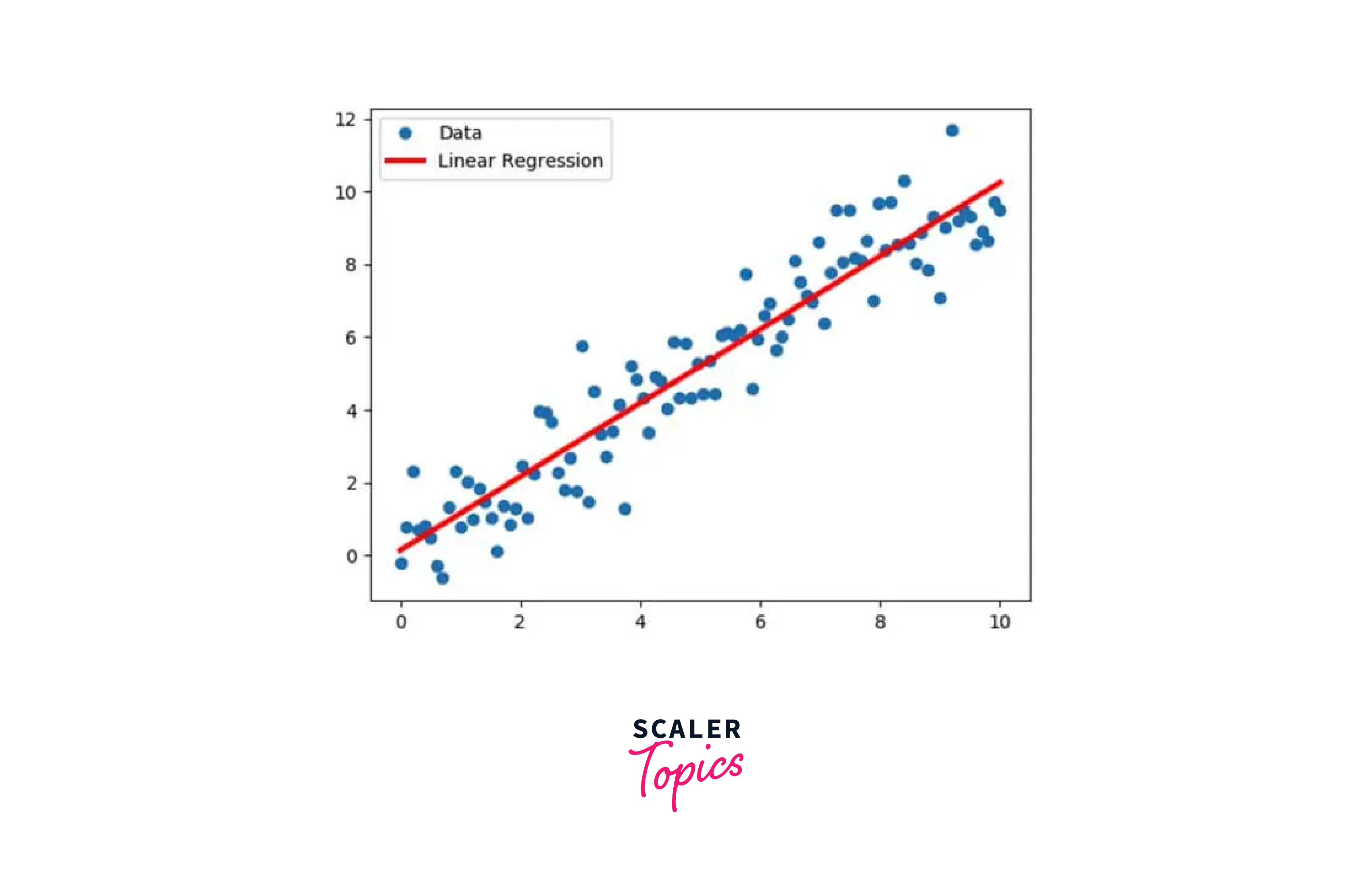
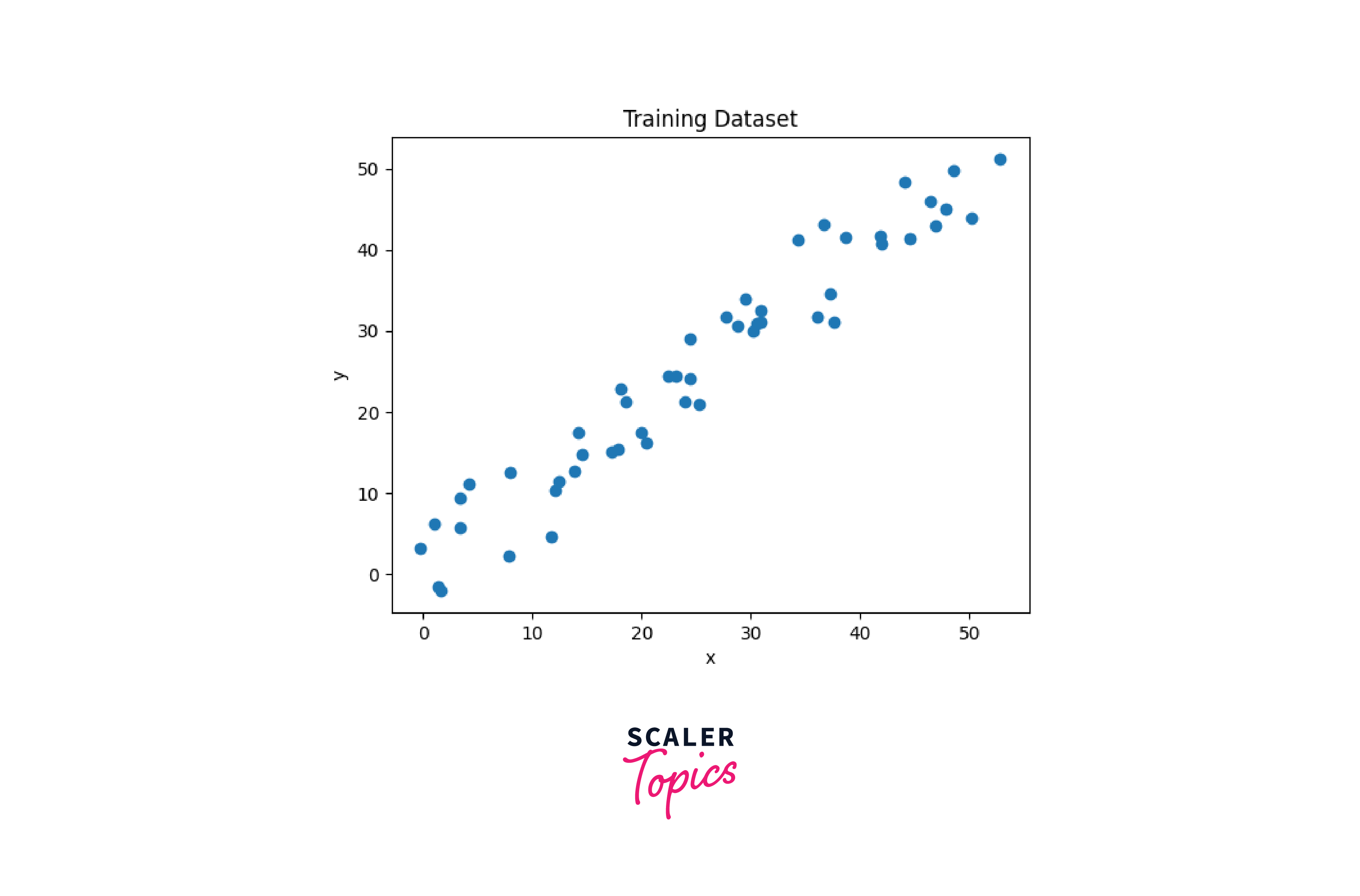
We collect and prepare the data for our tensorflow regression model. The np.linspace() function from the NumPy library is used to create an array of evenly spaced values. The below code generates 50 random points between 0 to 50.

To introduce randomness and simulate real-world scenarios, noise is added to the generated linear data. The np.random.uniform() function generates random numbers from a uniform distribution within a specified range. In this code, noise is added to both x and y by updating them with random values between -4 and 4.

Now, we will use Matplotlib to visualize the data,

Output:

Step 4: Train the Model

Next, we train the tensorflow regression model by defining a loss function and an optimization algorithm. We use TensorFlow's built-in functions to calculate the loss and update the model's parameters through backpropagation.

Output:

The hypothesis defines the predicted output ('y_pred') based on the input features ('X'), weight ('W'), and bias ('b'). It calculates the dot product of X and W, and then adds b to the result.

The mean squared error is a common cost function used in regression problems. It measures the average squared difference between the predicted output ('y_pred') and the actual target values ('Y').

Gradient descent is an optimization algorithm used to update the model's parameters (weights and biases) iteratively. It calculates the gradients of the cost function with respect to the model's variables and updates the variables accordingly to minimize the cost.

Step 5: Model Evaluation and Analysis

After training, we evaluate the performance of the tensorflow regression model on the training data.

Output:

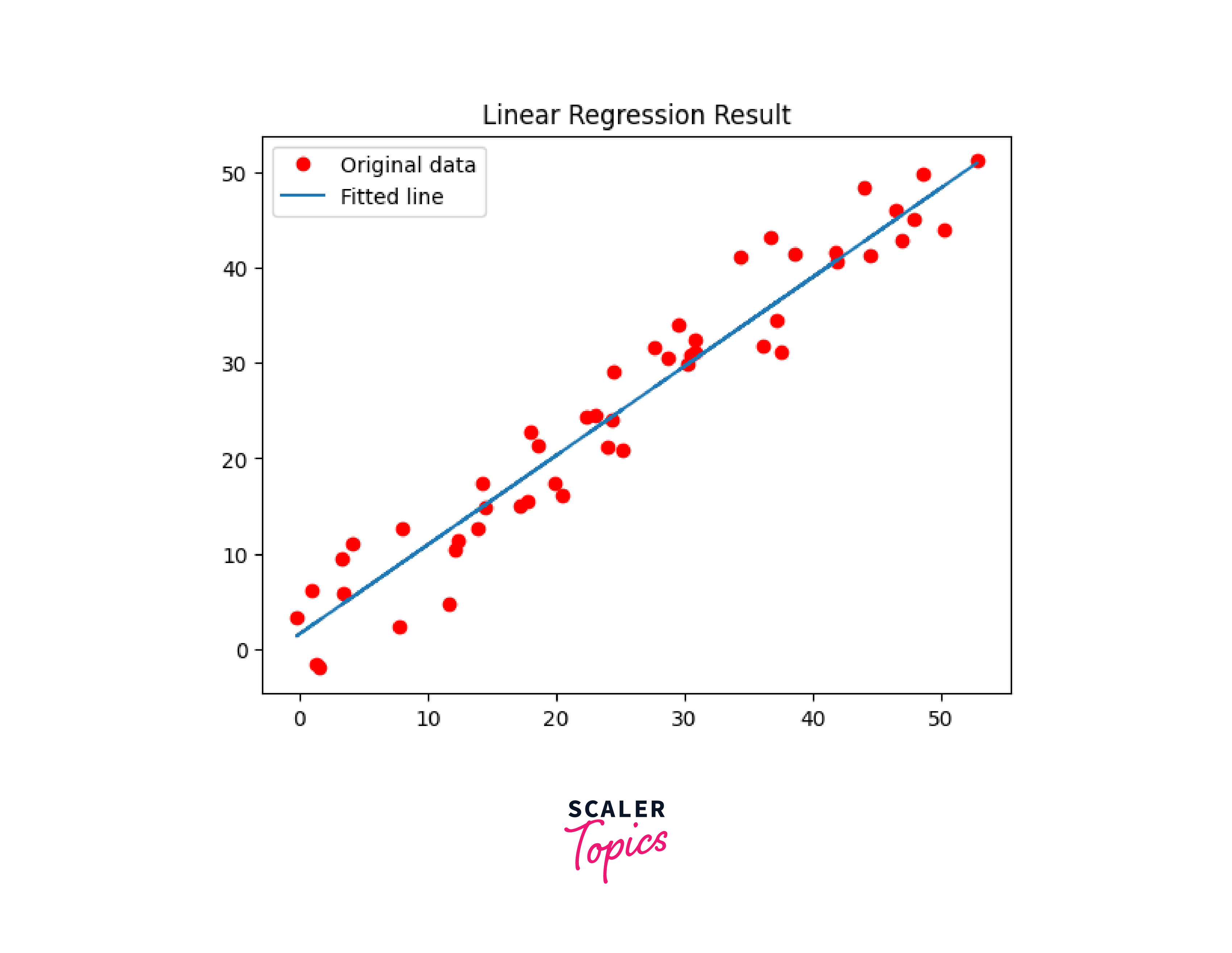
Step 6: Visualize the Results

We can plot the tensorflow regression line and the actual data points using Matplotlib to visualize the relationship between the variables.

Output:

Fine-tuning the Model

Fine-tuning a tensorflow regression model involves optimizing its hyperparameters and adjusting its configuration to enhance performance.

1. Cross-Validation and Hyperparameter Tuning:

   To fine-tune a tensorflow regression model, it is crucial to optimize its hyperparameters. One common approach is to use k-fold cross-validation, dividing the data into k subsets, and iteratively training and evaluating the model on different combinations of these subsets. TensorFlow's compatibility module provides functions and utilities, such as KFold or GridSearchCV, to implement cross-validation and hyperparameter tuning effectively. This code contains a Hyperband tuner, to instantiate the hyperband tuner, you must specify the maximum number of epochs to train.

2. Regularization Techniques:

   Regularization techniques help prevent overfitting and improve the model's generalization capabilities. Two popular regularization techniques for linear regression are L1 regularization (Lasso) and L2 regularization (Ridge). TensorFlow provides regularization functions, such as tf.nn.l1_regularizer() and tf.nn.l2_regularizer(), which can be incorporated into the model's cost function to add regularization terms. By tuning the regularization hyperparameter, we can control the impact of regularization on the model's performance.

   

3. Feature Selection and Engineering:

   Feature selection and engineering play a crucial role in improving the model's performance. TensorFlow provides methods and functions to evaluate feature importance, such as tf.feature_column.numeric_column() and tf.feature_column.bucketized_column(), which can help select relevant features or transform existing features into more informative representations.

   By carefully selecting and engineering features, we can enhance the model's predictive power and reduce the impact of irrelevant or noisy features.

4. Learning Rate and Optimization Algorithm:

   The learning rate determines the step size at which the optimization algorithm adjusts the tensorflow regression model's parameters. Fine-tuning the learning rate can significantly impact the model's convergence and accuracy.

   TensorFlow provides optimization algorithms, including gradient descent variants like Adam or RMSprop. Experimenting with different learning rates and optimization algorithms allows us to identify the combination that yields the best results for our specific problem.

5. Regular Monitoring and Model Evaluation:

   During fine-tuning, it is crucial to regularly monitor the model's performance and evaluate its effectiveness. TensorFlow provides tools for tracking metrics and visualizing performance using TensorBoard.

   Monitoring evaluation metrics such as mean squared error (MSE), R-squared, or validation loss allows us to identify when the tensorflow regression model begins to overfit or underperform, enabling us to adjust the fine-tuning strategies accordingly.

   By iteratively applying these fine-tuning strategies, we can optimize a Tensorflow regression model's hyperparameters, regularization, feature selection, learning rate, and optimization algorithm using the TensorFlow regression model. This iterative process allows us to refine the model's performance and improve accuracy and generalization on unseen data.