Transpose of a Matrix

Problem Statement

Given a 2D matrix having $n$ rows and $m$ number of columns. Print a transpose of the given matrix.

The transpose of a matrix is a new matrix that is obtained by exchanging the rows and columns.

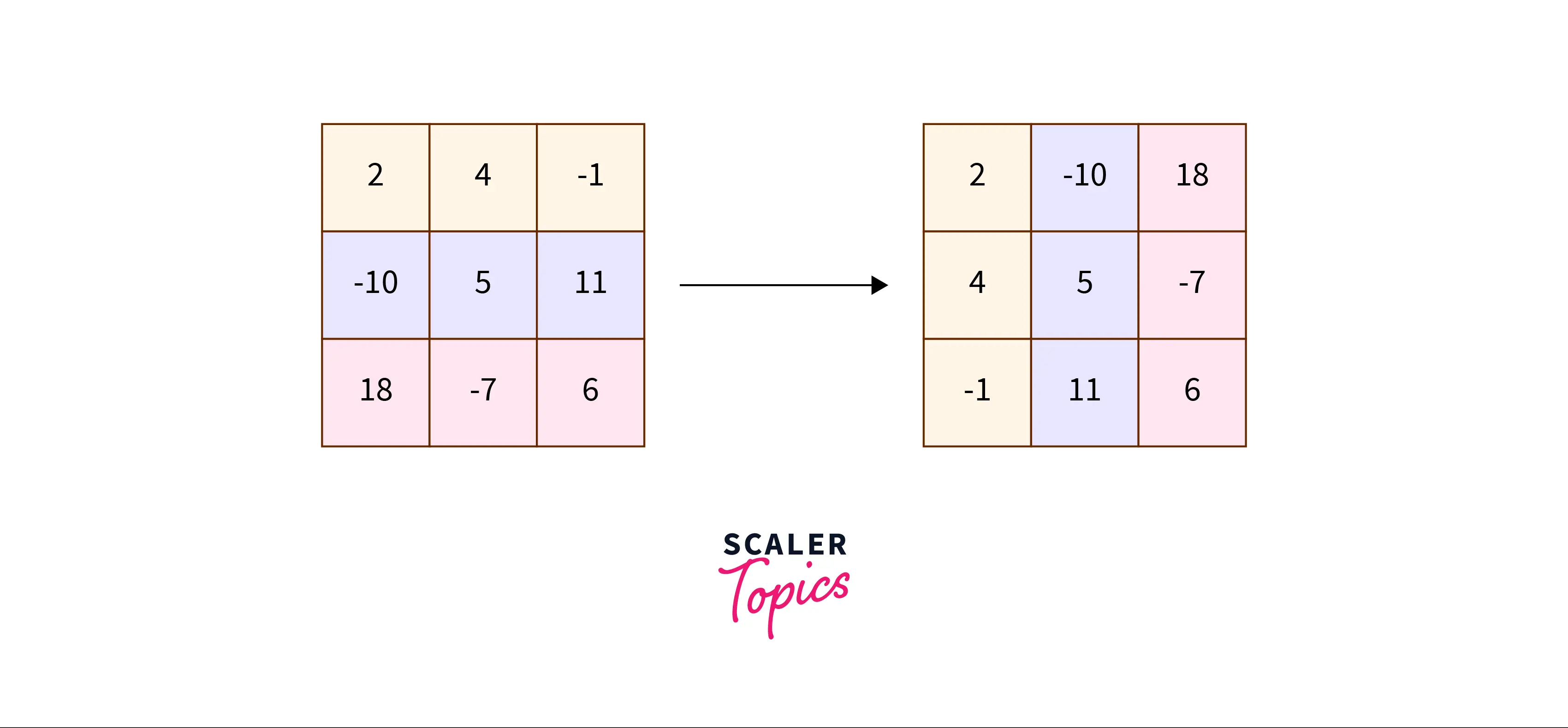
Example

Let us have a look at some examples on how to transpose a matrix.

Example1

Input:

Output:

Example2

Input:

Output:

Example Explanation

Let us have a look at some examples to understand how to transpose a matrix.

Example 1:

In this example, first the user enters the value of $n=2$ and $m=3$, followed by $n \times m = 2 \times 3 = 6$ numbers as input, i.e. $2\ 4\ 6\ -5\ 7\ 0$.

Hence the matrix formed is

$\begin{bmatrix} 2 & 4 \\ 6 & -5 \\ 7 & 0 \end{bmatrix}$

Once the code transposes this matrix, i.e. it interchanges the columns as rows and vice versa, the output becomes

$\begin{bmatrix} 2 & 6 & 7\\ 4 & -5 & 0 \end{bmatrix}$

This is the transpose of the given matrix.

Example 2:

In this example, first the user enters the value of $n=3$ and $m=3$, followed by $n \times m = 3 \times 3 = 9$ numbers as input, i.e. $1\ 2\ 3\ 4\ 5\ 6\ 7\ 8\ 9$.

Hence the matrix formed is $\begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix}$

Once the code transposes this matrix, i.e. it interchanges the columns as rows and vice versa, the output becomes

$\begin{bmatrix} 1 & 4 & 7\\ 2 & 5 & 8\\ 3 & 6 & 9 \end{bmatrix}$

This is the transpose of the given matrix.

Constraints

The following are the constraints assumed while we perform transpose of a matrix.

$n ==$ number of rows $m ==$ number of columns $1 <= m, n <= 1000$ $1 <= m * n <= 10^5$ $-10^9 <= matrix[i][j] <= 10^9$

Approach 1 - Using Functions - For Loop

Algorithm

1. Take input of $n$ and $m$
2. take input in matrix array of size $n \times m$.
3. create another transpose_matrix array of size $m \times n$ transpose of the input matrix.
4. Loop through the matrix array and convert its rows into columns of transpose_matrix array using transpose_matrix[ i ][ j ] = matrix[ j ][ i ];
5. print matrix array and transpose_matrix array which contains transpose of the matrix.

Code Implementation(in C++, java , python)

C++ implementation

Java implementation

python implementation

Output

Input

Output:

Time Complexity

The time complexity for transposing the matrix here will be $O(n^2)$ since we are using nested for loops to process the matrix array.

Space Complexity

The space complexity for transposing the matrix in this case will be $O(n^2)$ since we are using an extra matrix to store the result of the transpose operation.

Approach 2 - Without Using Function - Interchanging the Row and Column

Algorithm

1. Take input of $n$ and $m$
2. take input in matrix array of size $n \times m$.
3. print the matrix array.
4. loop for $n$ times a. In the $i$th loop, loop from $i+1$ element to $n$ times and swap the matrix[i][j] element with matrix[j][i] element
5. print matrix array that is now transposed.

Note: This algorithm will only work for square matrices having $n \times n$ dimension, i.e. $m==n$

Code Implementation(in C++, java , python)

C++ Code Implementation

Java implementation

Python implementation

Output

Input:

Output:

Time Complexity

The time complexity for the tranpose of the matrix here will be $O(n^2)$ since we are using nested for loops to process the matrix array.

Space Complexity

The space complexity for the transpose of the matrix in this case will be $O(1)$ since no extra space has been taken.