Transpose of a Matrix in C++

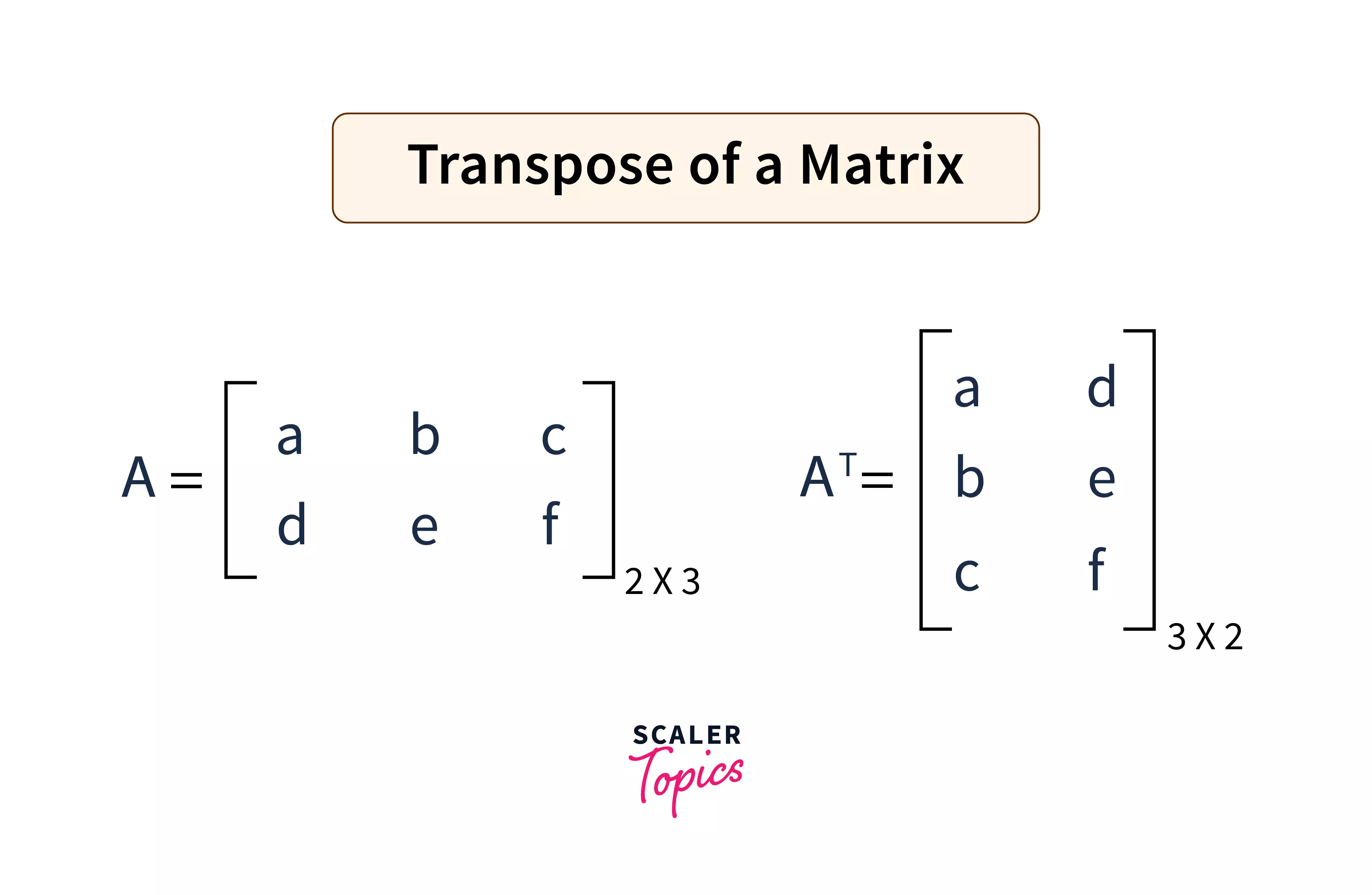
A transpose matrix is nothing but a new matrix obtained by interchanging rows of the original matrix with the columns of the original matrix.
In other words, we can say that the transpose matrix is obtained by flipping the matrix along the diagonal.
If a matrix initially of dimensions , then after the transposition, the dimensions would be . Please refer to the image below to visualize a matrix's transposition.
Example-
Let the matrix (say ) be
| 1 | 2 | 3 |
|---|---|---|
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 10 | 11 | 12 |
Now M transpose of will look like this -
| 1 | 4 | 7 | 10 |
|---|---|---|---|
| 2 | 5 | 8 | 11 |
| 3 | 6 | 9 | 12 |
You can notice that all the rows of are columns of , and columns of are rows of . Also, it can be seen that the dimensions of will be inverse to that of .
For example, if the dimension of is , then the dimension of will be .
Approach
The approach to find the transpose of a matrix in C++ is very easy; the steps needed to be followed are listed below -
- Let the given matrix be mat of dimension .
- Declare a 2-dimensional array say T_mat of dimension .
- Iterate from to and do the following -
- Iterate from to and perform -
- Print the obtained transposed matrix.
Pseudocode
Code Implementation
Program to Find Transpose of a Matrix in C++ Using Constant Space
To find the transpose of a matrix in C++ using constant space, you can follow a simple approach: swapping elements in-place without using any additional memory for a temporary matrix. Here's the code implementation:
Code Implementation:
Output:
Here's an example of the program's output:
Complexity:
The time complexity of this program is O(N^2), where N is the size of the square matrix. The space complexity is constant, O(1), because it uses only a few extra integer variables to perform the transpose operation in place.
Conclusion
- A matrix is a rectangular array of the same data types arranged in rows and columns.
- The transpose of a matrix is a matrix obtained by interchanging rows with columns. It is usually denoted by or
- If the dimension of the initial matrix was , then the dimension of the transposed matrix will be .
- Transpose of a matrix in C++ can be easily computed using nested loops.
